Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito RLC sem fonte

Ver Teoria
Exercício 61234578910

Enunciado

Determine i t para t > 0 no circuito abaixo.

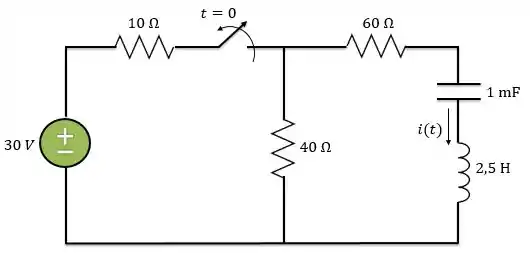
Passo 1

Vamos considerar que a chave estava fechada por um longo tempo antes de t = 0 . Logo, o circuito já estava em seu regime permanente, ou seja, já podemos considerar o indutor funcionando como curto circuito e o capacitor como um circuito aberto.

Passo 2

Logo, para o instante exatamente antes da chave se abrir ( t = 0 - ) , a gente pode considerar o circuito assim:

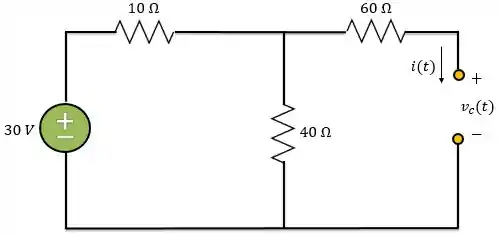
Como o circuito está aberto, não há circulação de corrente.

i 0 - = 0

Além disso, a tensão nos terminais do capacitor v c será a tensão nos terminais do resistor de 40   Ω .

v c 0 - = 40 40 + 10 × 30

v c 0 - = 24   V

Passo 3

Agora, vamos analisar o circuito quando a chave abre. Em t = 0 + , podemos considerar o seguinte circuito:

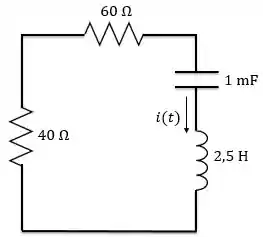
Esse circuito nós conhecemos! É o R L C série sem fonte!

Sendo R a soma dos resistores, já que estão em série.

Temos duas maneiras de encontrar a expressão para corrente i ( t ) . Vamos fazer das duas formas e você escolhe depois a que considerar melhor.

Aplicando a LTK no circuito, temos:

R i + L d i d t + 1 C ∫ - ∞ t i   d t = 0

Vamos eliminar a integral derivando a equação em relação a t .

R d i d t + L d 2 i d t 2 + 1 C i = 0

Agora, vamos dividir os termos por L e arrumar a equação.

d 2 i d t 2 + R L d i d t + i L C = 0

Substituindo os valores dos elementos, temos:

d 2 i d t 2 + 100 2,5 d i d t + i ( 0,001 ) ( 2,5 ) = 0

d 2 i d t 2 + 40 d i d t + 400 i = 0

Passo 4

Chegamos na equação diferencial de segunda ordem. Para resolver essa equação, primeiro vamos obter a equação característica:

r 2 + 40 r + 400 = 0

Resolvendo a equação do segundo grau, temos as duas raízes

r 1 = - 40 + 40 2 - 1600 2

r 1 = - 40 + 0 2

r 1 = - 20

e

r 2 = - 40 - 0 2

r 2 = - 20

Portanto, temos duas raízes reais, iguais e negativas:

r 1 = r 2 = - 20

Para esse caso a solução da EDO é

i t = A + B t e r 1 t

i t = A + B t e - 20 t

Essa é a primeira maneira!

Passo 5

Agora, vamos fazer de uma outra maneira mais rápida. Sabemos que em um circuito R L C série sem fontes:

α = R 2 L               e             ω 0 = 1 L C

Substituindo os valores dos elementos, temos:

α = 100 2 × 2,5 = 20

e

ω 0 = 1 ( 0,001 ) ( 2,5 ) = 20

Como α = ω 0 , temos o caso de amortecimento crítico e para esse caso a expressão da corrente é:

i t = A + B t e - α t

Substituindo o valor de α ,

i t = A + B t e - 20 t

Pronto! Essa é a segunda maneira.

Passo 6

Agora, precisamos encontrar os valores das constantes A e B . Como se trata de uma EDO de segunda ordem, precisamos da condição inicial da corrente i ( 0 + ) e de sua derivada d i ( 0 + ) / d t .

Nós já calculamos que:

i 0 - = 0

Como no indutor a corrente não varia instantaneamente, então:

i 0 - = i 0 + = 0

Portanto,

i 0 + = A + B ( 0 ) e - 20 ( 0 )

A = 0

Como o circuito é serie, a corrente é a mesma para todo o circuito e como no capacitor a tensão não pode variar instantaneamente:

v c 0 - = v c 0 + = 24   V

Logo, no indutor temos:

v L 0 + = L d i ( 0 + ) d t

Aplicando a LTK no circuito, temos:

R i 0 + + v c 0 + + v L 0 + = 0

v L 0 + = - v c 0 + - R i ( 0 + )

v L 0 + = - 24 - 100 0

v L 0 + = - 24   V

Isolando d i ( 0 + ) / d t ,

d i 0 + d t = 1 2,5 ( - 24 )

d i 0 + d t = - 9,6

Passo 7

Agora, vamos derivar a nossa expressão para a corrente do circuito.

i t = A + B t e - 20 t

Já sabemos que A = 0 . Logo,

i t = B t e - 20 t

Então, pela regra do produto, temos:

d i t d t = B e - 20 t + B t e - 20 t ( - 20 )

d i t d t = B e - 20 t - 20 B t e - 20 t

Usando a condição inicial para a derivada da corrente:

d i 0 + d t = B e - 20 ( 0 ) - 20 B 0 e - 20 0 = - 9,6

B = - 9,6

Passo 8

Portanto, substituindo os valores das constantes, nossa solução final será:

i t = 0 + ( - 9,6 ) t e - 20 t

i t = - 9,6 t e - 20 t     A

Resposta

i t = - 9,6 t e - 20 t     A

Exercícios de Livros Relacionados

Um circuito RLC em paralelo possui L = 2 H e C = 0,25 F. O valor de R que produzirá um fator de amortecimento unitário é:(a) 0,5 Ω (b) 1 Ω (c) 2 Ω (d) 4 Ω
A equação que descreve a tensão em um circuito RLC é d 2 v d t 2 + 5 d v d t + 4 v = 0 Se v(0) = 0, dv(0)/dt = 10 V/s, obtenha v(t).
Sabe-se que a corrente no circuito da Figura P6.35 é io = 2e-5.000t(cos 1.000t + 5 sen 1.000t) Apara t $ 0+. Determine v1(0+) e v2(0+).
Para o circuito da Figura 8.58, a corrente inicial no indutor (em t = 0) é:(a) 0 A (b) 2 A (c) 6 A (d) 12 A
Obtenha v ( t ) para t0 no circuito da Figura 8.73.