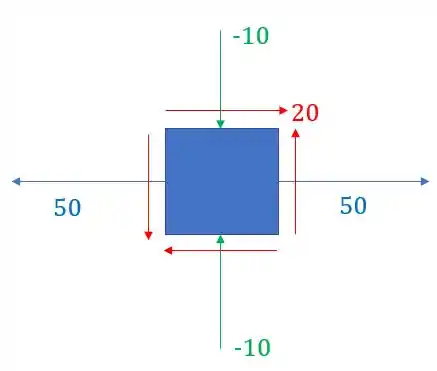
Abaixo é dado um círculo de mohr. Com base nele determine o valor das tensões , , e por fim desenhe o elemento infinitesimal relacioando a este círculo de mohr.
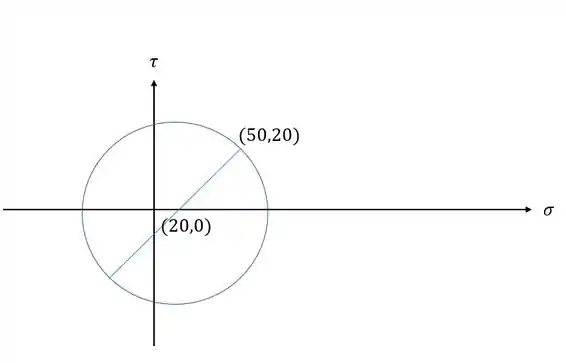
Passo 1
Antes de substituirmos qualquer valor vamos entender o que cada parte do nosso círculo de mohr representa.
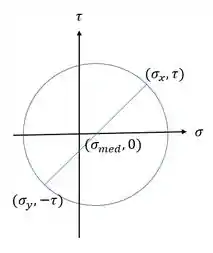
Sabemos que o valor central nós dá o valor de , o valor superior nos dará e o valor inferiro nos dará . Mas perceba que tanto o de cima quando o de baixo nós dará o valor de .
Passo 2
Agora que já definimos o que cada valor representa, basta tomar cuidado e definir facilmente cada um dos valores que nos é pedido.
Vamos analisar o triangulo que temos a partir do círculo de mohr.
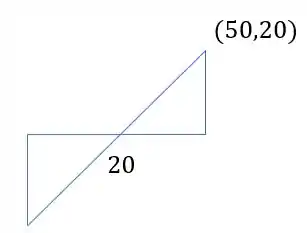
Definindo os valores de cada parte teremos, primeiro para parte superior do triangulo
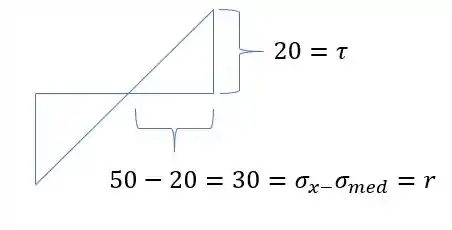
Em que podemos definir que
Analisando agora o triangulo abaixo teremos que
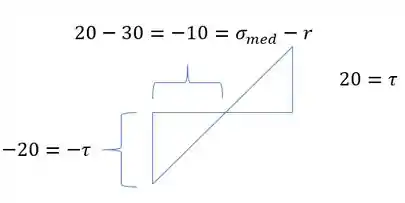
Em que podemos definir que
Ou seja, com o valor da tensão em y também confirmamos o valor do cisalhente.
Passo 3
Agora que já temos todos os valores, basta apenas desenhar o elemento, tomando cuidado com os sinais dos vetores.