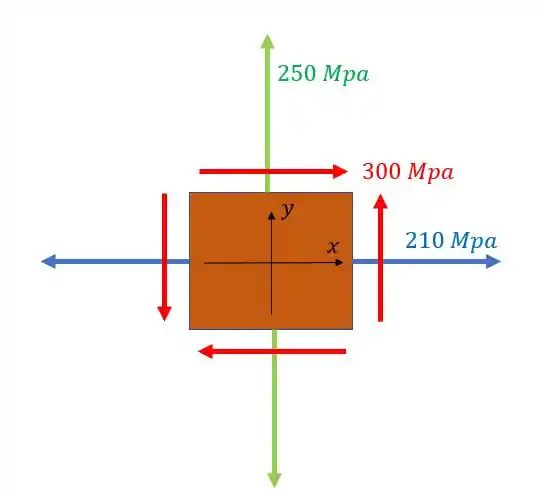
O elemento infinitesimal abaixo foi rotacionado de 57° no sentido anti-horário. Usando o círculo de Mohr, determine quais serão as tensões nesse plano a 57°.
Passo 1
Como já vimos queremos determinar alguns valores com base no círculo de mohr, e para fazermos isso precisamos desenhar o círculo de Mohr.
Sabemos que para fazer esse desenho necessitamos de dois pontos:
O primeiro é o ponto que marca o centro do círculo que é dado por
O segundo é o ponto que marca o fim do raio do círculo de mohr, que é dado por
Passo 2
Como já temos os valores para desenhar o círculo de mohr, vamos fazer os devidos desenhos e dessa forma começar a definir os valores pedidos no enunciado.
Sabemos que
Substituindo teremos que
Desenhando o círculo de mohr
Primeiro desenhamos o raio
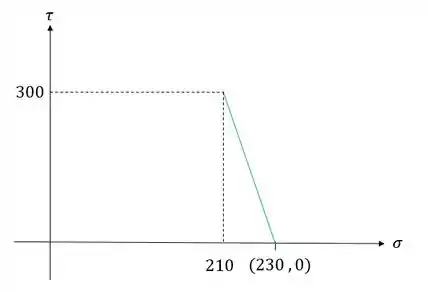
Depois desenhamos o círculo de mohr
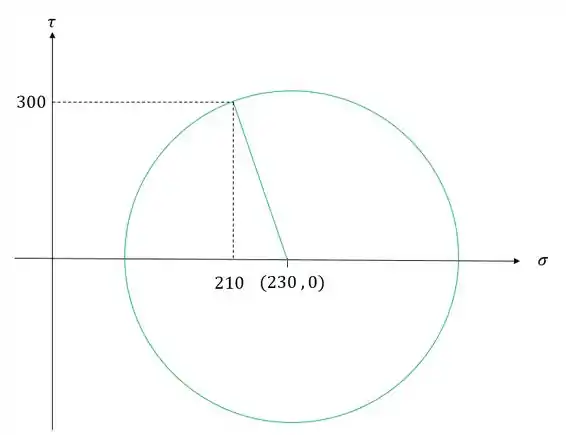
Passo 3
Agora que já temos o círculo de mohr precisamos lembrar como ele funciona quando fazemos a rotação do nosso elemento infinitesimal.
O primeiro conceito que temos que lembrar é que todo sentido que rotacionamos o nosso elemento é o contrario no círculo de mohr, por exemplo, se rotacionamos nosso elemento no sentido horário, no círculo de mohr faremos esse giro no sentido anti-horário e vice versa.
Outra coisa que precisamos saber é que no círculo de mohr o número de graus que andaremos será o dobro do número de graus que andamos no elemento, ou seja, no nosso caso andamos 57°, logo no círculo de mohr teremos que andar 114°.
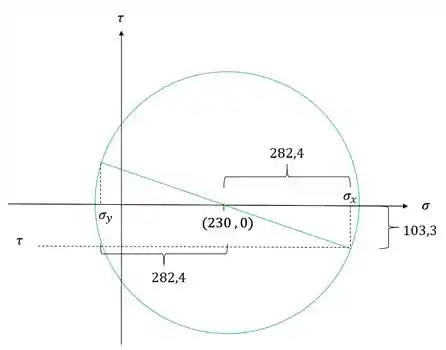
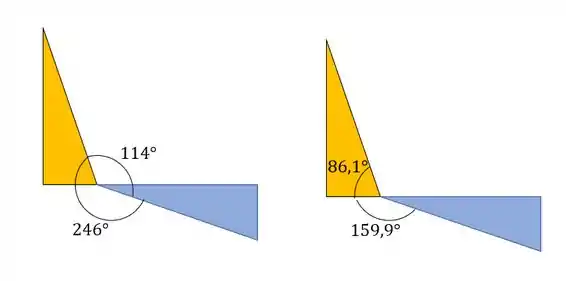
Juntando os dois conceitos teremos que rotacionar, a partir do raio que desenhamos o círculo de mohr, 114° no sentido horário. Na imagem abaixo podemos ver bem como devemos fazer isso.
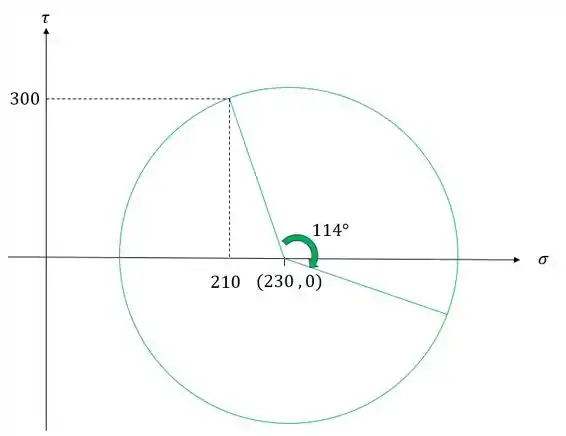
Outra coisa que precisamos notar são os dois triângulos da nossa figura, um triangulo para os valores iniciais e outro para os valores finais, que podemos ver abaixo
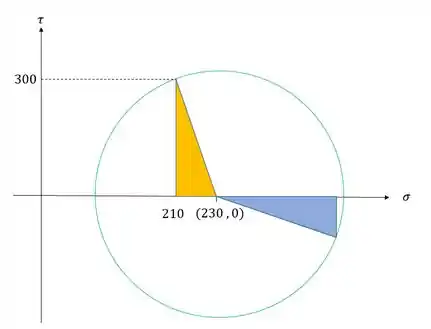
Sabemos que podemos determinar algumas coisas relacionadas aos triângulos,
Começando pelo triangulo amarelo sabemos que podemos determinar o valor dos catetos, como vemos na figura
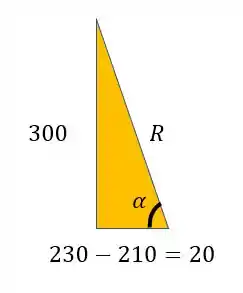
Se temos os valores dos catetos, podemos determinar facilmente o valor da hipotenusa pelo teorema de Pitágoras, lembrando que a hipotenusa do nosso triangulo simboliza exatamente o raio do nosso círculo de mohr.
Como já temos os valores dos catetos e da hipotenusa podemos também determinar o valor de , com isso teremos que
Mas porque calculamos esse ângulo? Veremos no próximo passo que ele nos ajudará nos cálculos do próximo triangulo, então vamos lá.
Passo 4
Como já analisamos o que tínhamos no triangulo amarelo, vamos ver agora o que conseguimos determinar no triangulo azul.
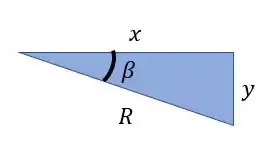
Dessas incógnitas sabemos que a hipotenusa desse triangulo também é o raio do nosso círculo, que já determinamos no passo anterior
Para determinarmos o valor de basta olharmos o seguinte
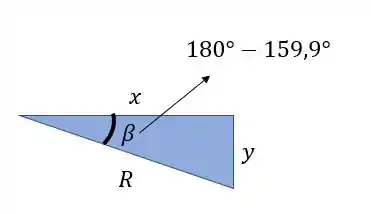
Com isso podemos ver que
Olhando o nosso triangulo teremos que usar relações trigonométricas para encontrarmos os valores desejados
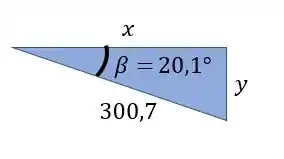
Sabemos que
Agora que já temos os valores vamos determinar o que eles representam no nosso círculo de mohr
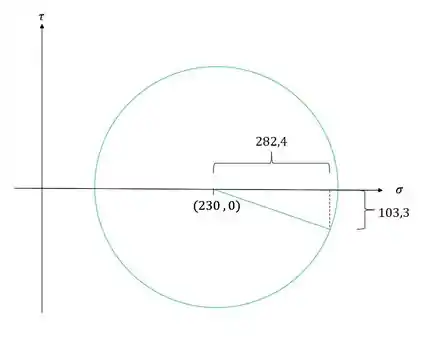
Pelo círculo de mohr teremos que
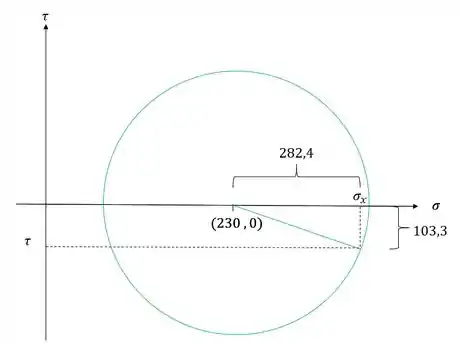
Para determinarmos a tensão normal em y basta analisarmos o prolongamento do raio
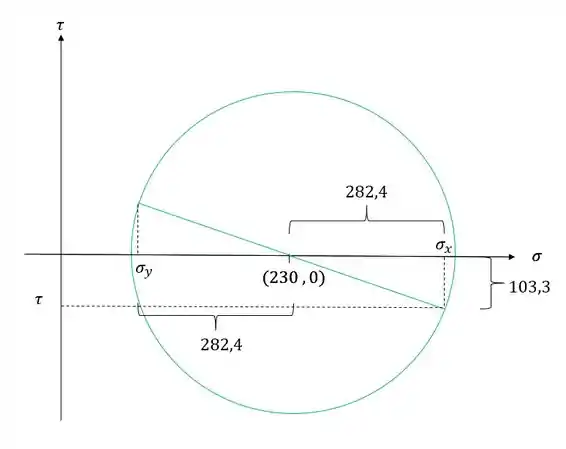
Como deu negativo significa que nosso círculo de mohr deveria ser mais para a esquerda como mostra figura