Uma barra de ferro, responsável por manter duas articulações juntas, possui resistência adimissivel para tensões normais de 51Mpa e a tensões cisalhantes de 45 Mpa.
Sabendo disso e que nesta barra em um certo momento foi retirando um elemento infinitesimal dado abaixo, determine se esta barra rompera, ou não. Se romper, será devido a qual das tensões?
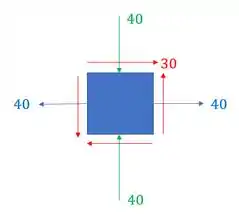
Passo 1
Como no exercício nos foi dado o valor das tensões admissíveis, precisamos determinar as tensões máximas que podem surgir nesse elemento, para isso dividiremos essa situação em duas partes.
Na primeira parte usaremos o círculo de Mohr para definirmos as tensões máximas existentes nesse elemnto.
Na segunda parte definiremos em que planos essas tensões máximas agem caso aja rompimento, se não houver rompimento não haverá necessidade de calcularmos os planos em que elas correm.
Passo 2
Como já vimos queremos determinar alguns valores com base no círculo de mohr, e para fazermos isso precismos desenhar o círculo de Mohr.
Sabemos que para fazer esse desenho necessitamos de dois pontos:
O primeiro é o ponto que marca o centro do círculo que é dado por
O segundo é o ponto que marca o fim do raio do círculo de mohr, que é dado por
Como já temos os valores para desenhar o círculo de mohr, vamos fazer os devidos desenhos e dessa forma começar a definir os valores pedidos no enunciado.
Sabemos que
Substituindo teremos que
Passo 3
Desenhando o círculo de mohr teremos que
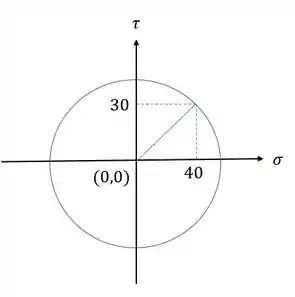
Como já temos o valor de basta apenas determinarmos o valor de R usando o triangulo retângulo da figura.
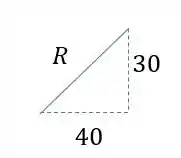
Fazendo essa conta teremos que
Logo
Passo 4
Agora precisamos ver todas as tensões máximas.
Primeiro vamos ver as normais
Como a resistência admissível para tensões normais é de 52Mpa, nosso material não romperá por tensões normais já que o máximo alcançado é de 50 Mpa.
Com relação a tensão cisalhante sabemos que o máximo alcançado é de exatamente o valor do raio do nosso círculo, logo o valor de .
Como a resistência do nosso material a tensões cisalhantes é de 45Mpa, ele romperá devido a tensão cislhante máxima. Mas em que plano?
Passo 5
Sabemos que a fórmula que nos dá o plano em que ocorrem as tensões principais é dado por
Substituindo os valores teremos que
O que é importante ressaltar aqui é que esses ângulos representam os planos em que ocorrem as tensões principais, e não a cisalhante, para descobrir a cisalhante é necessário somar e subtrair 45°
Logo os ângulos serão:
Ou
Resposta
O rompimento ocorre devido a tensão cisalhamte máxima de 50MPa e que ocorre nos planos de 63,5° ou -26,5°.