Obtenha o círculo de Mohr que descreve cada um dos seguintes estados de tensão:
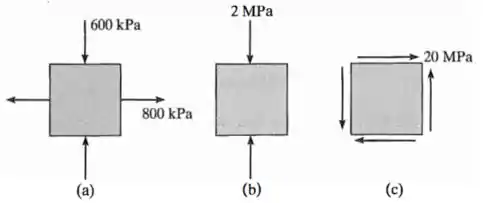
Passo 1
O exercício quer que a gente desenhe o Círculo de Mohr para cada um dos estados de tensão mostrados.
Então lembra aí!
Para desenhar um Círculo de Mohr, devemos começar definindo as tensões , e do estado de tensões.
Feito isso, vamos poder calcular a tensão normal média:
...para, em seguida, marcarmos os pontos e em um gráfico .
Aí, usando o primeiro ponto como o centro do círculo, podemos abrir um compasso até o segundo ponto e desenha o Círculo de Mohr!
Passo 2
Então vamos lá!
Começando pelo item :
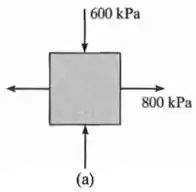
Nele, temos uma tração na horizontal de , uma compressão na vertical de , e nenhuma tensão de cisalhamento
Dessa forma, vamos ter que:
Agora, podemos calcular :
Desenhar os eixos e :
E em seguida marcar entre esses eixos os pontos e , ligar esses pontos e usá-los para desenhar nosso círculo:
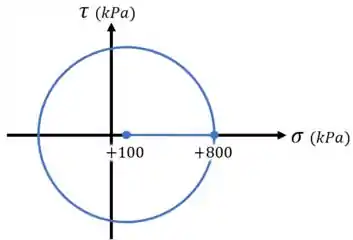
E pronto!
Item resolvido.
Passo 3
Agora, para o item :

Nós vamos ter:
Dessa forma, vai ser:
Aí, marcando esse ponto e o ponto em um gráfico , ligando esses pontos e usando eles para desenhar um círculo, vamos ter o desenho:
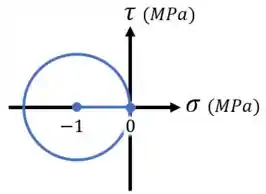
Que é a resposta do item .
Passo 4
E para o item :
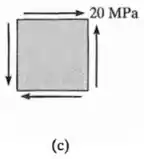
Temos:
De tal forma que:
Aí, marcando esse ponto e o ponto em um gráfico , ligando esses pontos e usando eles para desenhar um círculo, vamos ter:
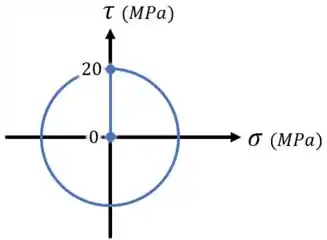
Que é a resposta do item .
E assim finalizamos o exercício!