Dado o elemento infinitesimal abaixo, determine o valor mínimo da tensão cisalhante em função da tensão no eixo x para que não ocorra rompimento do material que possui tensão admissível de 50Mpa para tensões normais.
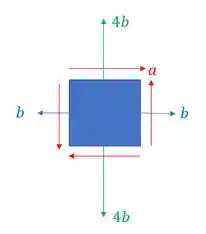
Passo 1
Como já vimos queremos determinar alguns valores com base no círculo de mohr, e para fazermos isso precismos desenhar o círculo de Mohr.
Sabemos que para fazer esse desenho necessitamos de dois pontos:
O primeiro é o ponto que marca o centro do círculo que é dado por
O segundo é o ponto que marca o fim do raio do círculo de mohr, que é dado por
Passo 2
Como já temos os valores para desenhar o círculo de mohr, vamos fazer os devidos desenhos e dessa forma começar a definir os valores pedidos no enunciado.
Sabemos que
Substituindo teremos que
Passo 3
Desenhando o círculo de Mohr teremos que
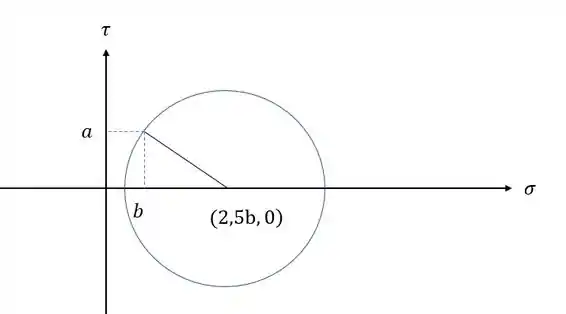
Olhando o nosso triangulo teremos que
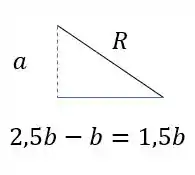
Fazendo pitagora teresmo que
As nossas tensões principais são dadas por
Em que
E nesse caso como queremos saber o limite do rompimento, usaremos
Substituindo tudo teremos que
Isolando a raiz, teremos que
Elevando os valores de ambos os lados ao quadrado teremos que
Isolando cada letra de um lado teremos que
Podemos simplificar essa solução escrevendo a solução como