Para o estado de tensão mostrado na figura, determine, usando Círculo de Mohr, a tensão normal e a tensão de cisalhamento atuantes no plano .
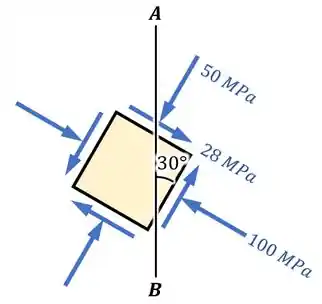
Passo 1
O que está acontendo?
O exercício nos forneceu um estado plano de tensões, para o qual podemos definir eixos e :
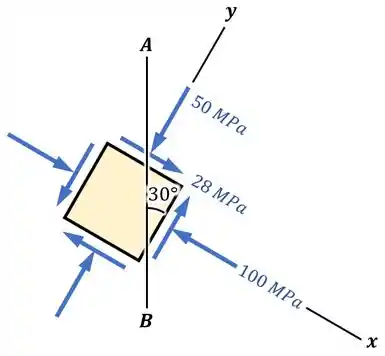
Fazendo isso, conseguimos definir as tensões:
E o que é que o exercício quer?
Basicamente, ele quer que a gente faça uma transformação de tensões.
Ele quer que a gente rotacione o elemento por um ângulo :
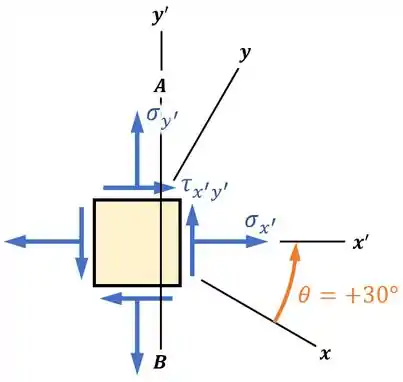
Ao fazemos isso, as novas tensões e que vão surgir vão corresponder (ser iguais) às tensões normal e cisalhante no plano , que é o que o exercício quer saber.
O exercício ainda quer que a gente resolve ele usando o Círculo de Mohr.
Então para resolver o exercício...
Devemos usar as tensões , & para desenhar um círculo de Mohr para esse elemento.
Feito isso, vamos rotacionar a reta do círculo de Mohr que diz as tensões no nosso eixo ( e ) por um ângulo , definindo assim as tensões num eixo ( e ).
Em seguida, vamos usar trigonometria (seno, cosseno, etc.) para decifrar os valores de e .
Por fim, esses valores vão corresponder às tensões e no plano pedidas pelo exercício, sendo assim as nossas respostas para o exercício.
Passo 2
Então vamos começar desenhando o nosso círculo de Mohr!
Lembra aí!
Já definimos as , & , então o próximo passo para desenhar o círculo de Mohr é calcular o valor de :
Agora, podemos desenhar os eixos e :
E marcar nele os pontos:
- ;
- & .
Marcados esses pontos, ligamos ele com uma reta e desenhamos o nosso círculo:
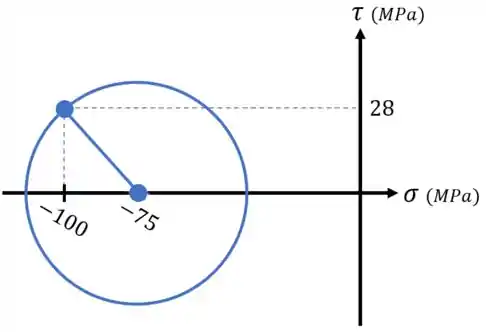
Passo 3
Agora, vamos rotacionar a reta do nosso círculo de Mohr usando um ângulo .
Aqui, devemos nos lembrar que:
- Enquanto que o ângulo no estado de tensões é positivo no sentido anti-horário;
- O ângulo no círculo de Mohr é positivo no sentido horário.
(Isso só não ocorre caso a gente opte por desenhar desde o começo o gráfico do Círculo de Mohr com o eixo apontando para baixo.)
Se lembrando disso, percebemos que essa rotação vai ser então uma rotação de no sentido horário:
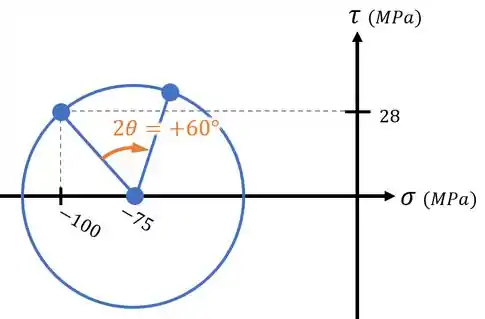
Aí, enquanto que a reta antiga definia as tensões antigas ( e ) no eixo , a reta nova vai definir as tensões novas ( e ) no eixo rotacionado :
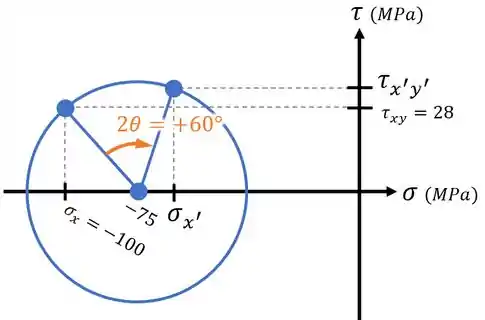
Passo 4
Definidas as tensões e no gráfico, precisamos agora usar trigonometria para encontra-las.
Para tanto, vamos focar no desenho abaixo, montado a partir dos dados do círculo de Mohr acima:
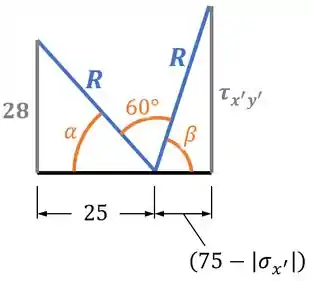
Primeiro, fazendo Pitágoras no triângulo esquerdo, temos:
O que significa que:
Além disso, podemos ver que a tangente do ângulo é:
Aí, colocando esse valor na função da nossa calculadora, encontramos que:
Em seguida, podemos perceber que:
Aí, isolando e substituindo , encontramos que:
Agora, podemos usar seno de para encontrarmos o valor de :
Isolando e substituindo e , encontramos que:
Calculando, isso dá:
Além disso, ainda podemos usar o cosseno de para encontrarmos o valor de :
Aí, isolando e substituindo e , encontramos:
O que dá:
Em seguida, isolando , encontramos que:
E por fim, como no gráfico é negativo, isso significa que:
E pronto!
Nosso exercício está resolvido, e, para fornecermos a nossa resposta, basta fazermos a correspondência das tensões encontradas para o eixo com as tensões no plano :