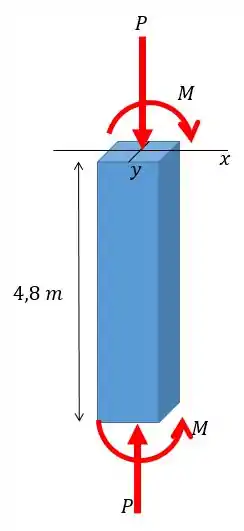
A coluna de aço estrutural está engastada no topo e na base. Se suportar os momentos nas extremidades, determine a força axial que pode ser aplicada. Ocorre flexão em torno do eixo . Use as equações da seção 13.6 e a equação 13.30.
Passo 1
Fala aí, pessoal!! Este problema pede para fazermos uma verificação de falhas da coluna através do método da tensão admissível (que é a equação 13.30 a qual o problema se refere) e tem o seguinte formato:
O problema pede para fazermos a análise tanto do momento quanto da força compressiva, então a gente vai montar o probleminha todo e lá no final vamos fazer essa análise tudo junto, beleza?
Para calcular essa tensão admissível nós vamos utilizar a tabela de equações :

Então vamos calcular o índice de esbeltez, aplicar a equação correspondente e achar . Depois é só substituir na primeira equação e vamos ver se a coluna falha ou não =D
Passo 2
Vamos começar calculando o índice de esbeltez da coluna
Como a coluna está engastada na base e no topo temos que , a altura da coluna é , agora falta achar o raio de giração , que pode ser achado através da relação entre o momento de inércia e a área.
O momento de inércia é o do perfil , lembrando que para calcular o raio de giração precisamos do menor momento de inérica. Assim temos que
E a área
Sendo assim vamos ter o raio de giração
Logo, podemos calcular o valor do índice de esbeltez:
E o índice de esbeltez comparativo. Esse valor é inerente ao material, não dependendo da geometria da coluna:
Aqui a gente tem que olhar nas tabelas para o aço e achar:
Show! Agora temos os dois valores e podemos utilizar a tabela para fazer a comparação e saber qual equação utilizar.
Passo 3
A tabela é a seguinte.

Como a gente já calculou os dois índices de esbeltez, basta comparar os termos e vamos ter:
Logo,
Ou seja, vamos utilizar a segunda equação para o cálculo da tensão admissível.
É claro que temos que calcular antes, logo:
Assim, vamos ter:
Agora podemos calcular o valor da tensão admissível
Logo, vamos obter
Passo 4
Agora podemos aplicar a equação do método da tensão admissível.
Para a tensão de flexão vamos precisar do momento de inércia e da distância . O próprio problema nos diz que a flexão ocorre em torno do eixo logo, tirando da tabela de perfis de abas largas para o perfil :
E o valor de é a metade da altura (na tabela a altura é mesmo! kkk)
O resto dos valores nós já temos então vamos substituir na equação
Utilizando os dados em e vamos ter:
Se lembram que a gente tinha que analisar pelo momento e pela força? Então, olha como o momento impõe uma tensão de , que é menor do que a admissível de . Sendo assim, podemos calcular a força que vai valer:
Resposta
A coluna resiste ao momento aplicado e ainda suporta uma carga compressiva de: