A coluna de aço estrutural suporta uma carga axial de além de uma carga excêntrica . Determine se a coluna falhará com base nas equações da seção 13.6 e a equação 13.30. Considere que a coluna está engastada na base e que seu topo está livre para oscilar no plano enquanto preso por pinos no plano .
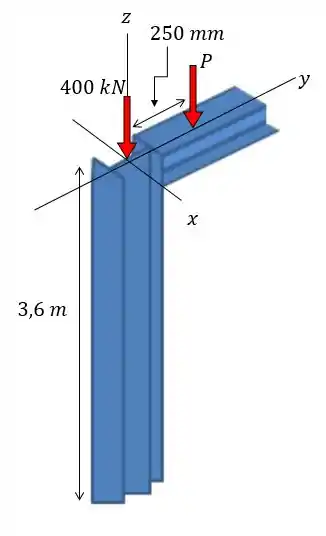
Passo 1
Fala aí, pessoal!! Este problema pede para verificarmos se a coluna falhará devido aos carregamentos nela exercidos. Para isso a gente tem que lembrar que a coluna pode falhar por flambagem ou por escoamento devido à compressão.
Mas antes da gente sair resolvendo que tal lembrar das equações as quais o problema se referiu? São elas:
- Equações da seção 13.6: são aquelas empíricas para diversos tipos de materiais e índices de esbeltez. Como nós temos uma coluna de aço então essas equações vão ser as seguintes.
- Já a equação 13.30 é a equação quando utilizamos o método da tensão admissível e é dada por.

Então para resolver esse problema a gente vai calcular o índice de esbeltez para saber qual equação da tabela utilizar para o . Com isso vamos substituir nessa última equação acima e finalmente ver se a coluna aguenta ou não o carregamento.
Passo 2
Vamos começar calculando o índice de esbeltez da coluna
Como a coluna está engastada na base e livre no topo temos que , a altura da coluna é , agora falta achar o raio de giração , que pode ser achado através da relação entre o momento de inércia e a área.
O momento de inércia é o do perfil , lembrando que para calcular o raio de giração precisamos do menor momento de inérica. Assim temos que
E a área
Sendo assim vamos ter o raio de giração
Logo, podemos calcular o valor do índice de esbeltez:
E o índice de esbeltez comparativo. Esse valor é inerente ao material, não dependendo da geometria da coluna:
Aqui a gente tem que olhar nas tabelas para o aço e achar:
Show! Agora temos os dois valores e podemos utilizar a tabela para fazer a comparação e saber qual equação utilizar.
Passo 3
A tabela é a seguinte.

Como a gente já calculou os dois índices de esbeltez, basta comparar os termos e vamos ter:
Logo,
Dessa forma nós vamos utilizar a primeira equação para o cálculo da tensão admissível.
Onde é dado por:
Assim, vamos ter:
Agora podemos calcular o valor da tensão admissível
Logo, vamos obter
Passo 4
Agora podemos aplicar a equação do método da tensão admissível.
Para a tensão de flexão vamos precisar do momento de inércia e da distância . Porém aqui nós temos de perceber que a flexão ocorre em torno do eixo . Logo, tirando da tabela de perfis de abas largas para o perfil :
E o valor de é a metade da altura (na tabela a altura é mesmo! kkk)
O resto dos valores nós já temos então vamos substituir na equação
Aí aqui só pra lembrar que a força compressiva vale:
E o momento:
Vejam que chegamos num absurdo, logo a coluna não suporta esse carregamento e falhará por flambagem!
Resposta
Vejam que chegamos num absurdo, logo a coluna não suporta esse carregamento e falhará por flambagem!