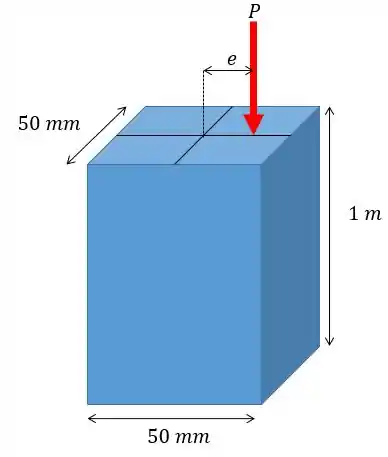
Uma coluna de aço engastada na base e livre no topo sofre um carregamento deslocado de do eixo central como mostrado na figura. Determine se essa coluna é segura com base no método da interação. Dados: . Tensões admissíveis ; .
Passo 1
Como podemos ver o problema está falando sobre flambagem no caso de uma carga excêntrica e pede para verificarmos se a carga aplicada à coluna está acima ou abaixo do limite permitido, o problema pede para que façamos essa análise com base no método da interação.
Com isso a gente pode verificar alguns pontos:
- A seção transversal é um quadrado e, portanto, tem o mesmo momento de inércia para ambos os eixos. Sendo assim não precisamos nos preocupar com o eixo onde ocorre a flambagem.
- Nós temos de utilizar a tabela experimental para colunas de aço dado abaixo, sendo assim precisamos achar o valor do índice de esbeltez para saber qual equação utilizar.
- Utilizando a equação correta da tensão admissível
Passo 2
Vamos começar calculando o índice de esbeltez da coluna
Como a coluna está engastada na base e livre no topo temos que , a altura da coluna é , agora falta achar o raio de giração , que pode ser achado através da relação entre o momento de inércia e a área.
O momento de inércia do nosso quadrado é
E a área
Sendo assim vamos ter o raio de giração
Logo, podemos calcular o valor do índice de esbeltez:
E o índice de esbeltez comparativo. Esse valor é inerente ao material, não dependendo da geometria da coluna:
Show! Agora temos os dois valores e podemos utilizar a tabela para fazer a comparação e saber qual equação utilizar.
Passo 3
A tabela é a seguinte.

Como a gente já calculou os dois índices de esbeltez, basta comparar os termos e vamos ter:
Logo,
Ou seja, vamos utilizar a primeira equação para o cálculo da tensão admissível.
Logo, vamos obter
Passo 4
Agora podemos aplicar a equação da interação:
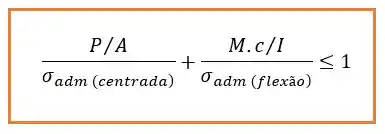
Aqui nós não temos nem o momento nem o valor de , então vamos calcular o momento a partir do valor da força excêntrica da forma
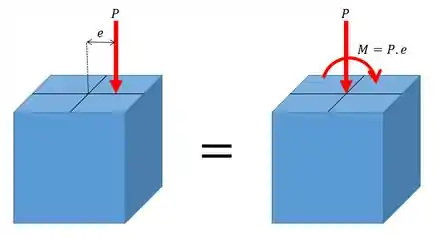
Como e
O valor de é igual a maior distância da linha neutra até a superfície da peça. Olhando a seção transversal nós vamos ter
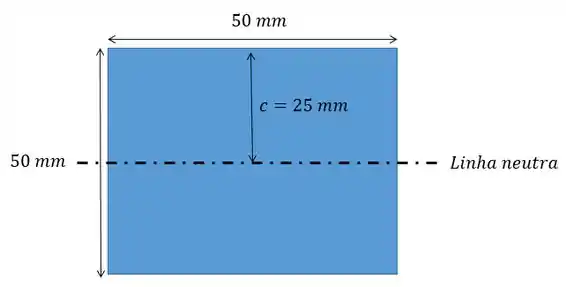
Sendo assim
O resto dos valores nós já temos então vamos substituir na equação
Então por enquanto está tudo certinho!
Passo 5
A gente só precisa fazer uma última verificação. Isso acontece porque algumas normas dizem que esse método da interação só pode ser utilizado quando:
Substituindo
Agora deu ruim! Então veja como isso é importante, utilizando essa norma a coluna até passa no teste. Mas a grande questão é que esse norma não pode ser utilizada nesse caso devido à elevada carga centrada!
Resposta
Apesar da coluna passar no teste do método da integração, este método não pode ser utilizado devido à elevada carga centrada.