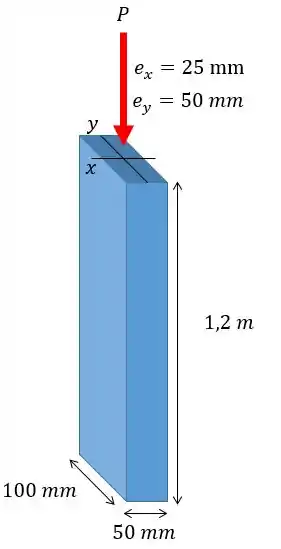
Determine a carga excêntrica máxima admissível que pode ser aplicada à coluna de madeira engastada na base e livre no topo. Utilize o método da tensão máxima admissível e a seguinte tabela como base.

Passo 1
Faala, galerinha! Agora a gente pode ver que o problema nos traz uma força ecêntrica com relação à dois eixos. Desta forma a gente vai ter duas tensões de flexão, ok?
Então para resolver esse problema a gente vai:
- Dividir a força excêntrica em uma força centrada mais dois momentos.
- Calcular as respectivas tensões (uma axial e duas de flexão).
- Calcular a tensão admissível.
- Comparar o valor da tensão máxima com a tensão admissível.
Passo 2
Vamos fazer um desenho então para ver como a nova força e os momentos vão ficar:
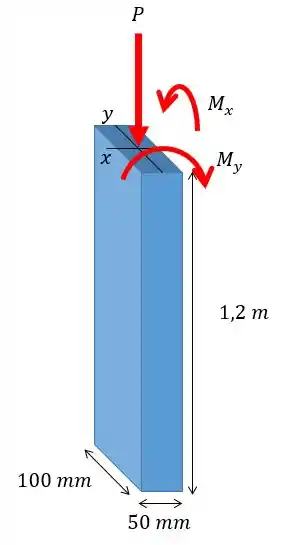
Vamos achar o valor de cada momento fazendo:
Então vamos ter:
Pessoal! A força vertical será a responsável pela tensão axial enquanto os momentos pelas tensões de flexão!
Passo 3
Para achar a tensão axial é só pegar a carga centrada e dividir pela área:
Calculando a área:
Substituindo a gente vai ter:
Como a gente não tem o valor de então vamos deixar assim =D
Passo 4
As componentes de flexão vão ser dadas por:
Calculando a tensão de flexão no eixo a gente vai ter:
A gente já tem o momento em :
Podemos calcular o momento de inércia em :
E o valor de
substituindo vamos achar:
Passo 5
Agora vamos calcular o valor da a flexão em :
A gente já tem o momento em :
Podemos calcular o momento de inércia em :
E o valor de
substituindo vamos achar:
Passo 6
Beleza, galera a gente já achou as tensões que atuam na coluna:
Agora vamos ver se a coluna aguenta essas tensões!!
Para qualquer dos métodos que podemos utilizar a primeira coisa que temos de fazer é calcular o índice de esbeltez. Tal índice é calculado a partir do comprimento , fator de comprimento efetivo e o raio de giração :
Pessoal, o comprimento já foi dado e vale , como a coluna está engastada na base e livre no topo temos que e o raio de giração é obtido a partir da seguinte equação entre o momento de inércia e a área:
A gente já calculou ambos os momentos de inércia, a gente só precisa lembrar que temos de utilizar o menor de forma a obter o menor valor para o raio de giração.
Para ter o menor raio de giração vamos ter que utilizar:
Substituindo na equação para achar o valor do raio de giração:
Agora podemos achar o valor do índice de eslbetez!
Passo 7
Galera, a gente já ta no final da resolução desse exercício. Agora vamos calcular a tensão admissível, para isso vamos utilizar a tabela para a madeira que foi até dada no problema mas é a seguinte:

Observe que o valor do índice de esbeltez é maior do que 55:
Logo vamos ter que utilizar a terceira equação:
Aí é só substituir né pessoal!
Para esse método a gente precisa achar a tensão máxima e comprar acom a tensão admissível . A tensão máxima é dada pela soma da axial com a de flexão:
Passo 8
A última coisa a ser feita agora é igualar à .
Resposta
O maior valor da força que pode ser aplicada à coluna é de