A coluna de alumínio com perfil está sob uma carga de aplicada de modo excêntrico conforme a figura. Sabendo que essa coluna está engastada na base e livre no topo, verifique se a coluna resiste à carga aplicada segundo o método da tensão admissível.
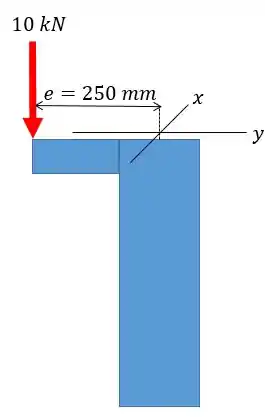
Passo 1
Pessoal, esse exercício é quase igual ao anterior. A única diferença é que agora a gente vai saber se essa coluna vai resistir ou não, ao invés de só calcular as tensões que atuam nela.
Então se você já viu o exercício anterior e entendeu pode pular para os passos 2,3 e4. Se você não viu o exercício anterior não tem problema, é só acompanhar todos os passos =D
Vamos lembrar que:
- Tensão axial – Essa tensão é fornecida pela equação da carga centrada (aquela da tabela).
- Tensão de flexão – Essa tensão é calculada pela equação
Passo 2
A gente acabou de ver que vamos ter duas tensões, correto? A axial e a de flexão. Vamos ver como isso funciona um pouco melhor fazendo a transformação de uma força excêntrica em uma força centrada mais um momento:
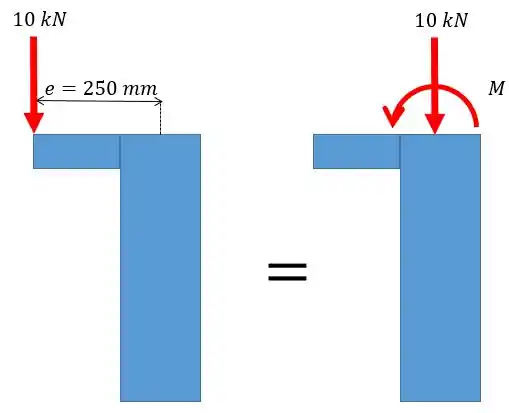
A gente precisa só saber qual o valor desse momento, não é mesmo? Ele vai ser dado pela força vezes a distância .
Pessoal! A força vertical será a responsável pela tensão axial enquanto o momento pela tensão de flexão!
Passo 3
Para achar a tensão axial é só pegar a carga centrada e dividir pela área:
A força vale e a área é tabelada para o perfil :
Substituindo a gente vai ter:
Passo 4
Mas não existe apenas o componente axial, correto? Temos que calcular o componente axial também! Essa componente é dada por:
O momento a gente já calculou lá no passo 2 e vale:
A tensão vai ocorrer no eixo em torno do eixo então temos que ter o momento de inércia em relação à esse eixo:
Falta só o valor de , para isso a gente precisa olhar o perfil da nossa coluna :
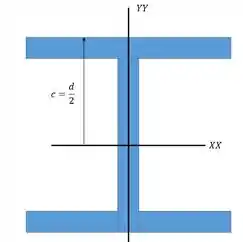
No caso desse tipo de perfil a gente vai ter quase sempre que é metade da altura . Para esse perfil temos que:
Assim,
Agora basta substituir na equação da tensão de flexão:
Passo 5
Beleza, galera a gente já achou as tensões que atuam na coluna:
Agora vamos ver se a coluna aguenta essas tensões!!
Para qualquer dos métodos que podemos utilizar a primeira coisa que temos de fazer é calcular o índice de esbeltez. Tal índice é calculado a partir do comprimento , fator de comprimento efetivo e o raio de giração :
Pessoal, o comprimento já foi dado e vale , como a coluna está engastada na base e livre no topo temos que e o raio de giração é obtido a partir da seguinte equação entre o momento de inércia e a área:
Como estamos tratando com um perfil vamos ter que:
Pessoal, lembrem-se que a gente precisa sempre utilizar o menor raio de giração!! Então temos que utilizar o menor momento de inércia para esse cálculo:
Substituindo na equação para achar o valor do raio de giração:
Agora podemos achar o valor do índice de eslbetez!
Passo 6
Galera, a gente já ta no final da resolução desse exercício. Agora vamos calcular a tensão admissível, para isso vamos utilizar a tabela para o alumínio que é a seguinte:
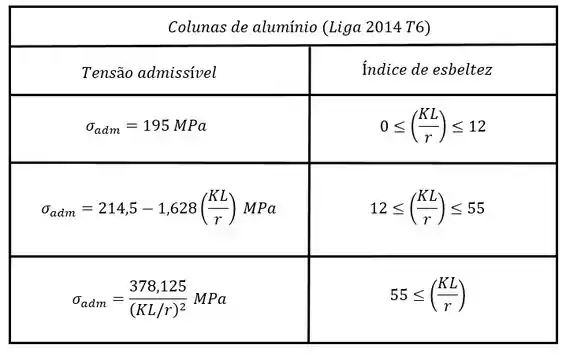
Observe que o valor do índice de esbeltez é maior do que 55:
Logo vamos ter que utilizar a terceira equação:
Aí é só substituir né pessoal!
Para esse método a gente precisa achar a tensão máxima e comprar acom a tensão admissível . A tensão máxima é dada pela soma da axial com a de flexão:
Observe que está bem acima do limite da tensão admissível
Portanto essa coluna não irá resistir ao esforça da força!!!
Resposta
Observe que está bem acima do limite da tensão admissível
Portanto essa coluna não irá resistir ao esforça da força!!!