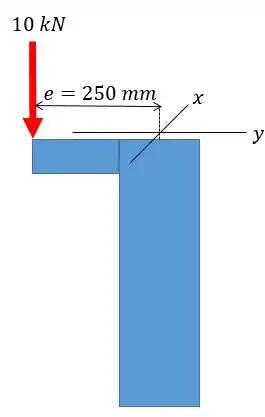
A coluna de alumínio com perfil está sob uma carga de aplicada de modo excêntrico conforme a figura. Sabendo que essa coluna está engastada na base e livre no topo, calcule o valor da tensão axial e da tensão de flexão atuantes na viga.
Passo 1
Fala aí, galera!! Esse tópico exige muitas contas então vamos começar com um exercício um pouco mais simples e vamos calacular as duas tensões que agem na nossa viga.
- Tensão axial – Essa tensão é fornecida pela equação da carga centrada (aquela da tabela).
- Tensão de flexão – Essa tensão é calculada pela equação
Por enquanto é isso que precisamos saber!
Passo 2
A gente acabou de ver que vamos ter duas tensões, correto? A axial e a de flexão. Vamos ver como isso funciona um pouco melhor fazendo a transformação de uma força excêntrica em uma força centrada mais um momento:
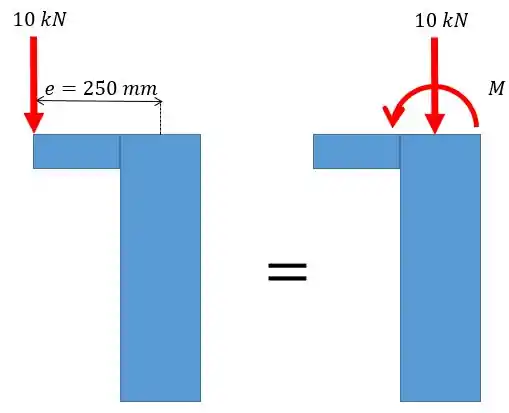
A gente precisa só saber qual o valor desse momento, não é mesmo? Ele vai ser dado pela força vezes a distância .
Pessoal! A força vertical será a responsável pela tensão axial enquanto o momento pela tensão de flexão!
Passo 3
Para achar a tensão axial é só pegar a carga centrada e dividir pela área:
A força vale e a área é tabelada para o perfil :
Substituindo a gente vai ter:
Passo 4
Mas não existe apenas o componente axial, correto? Temos que calcular o componente axial também! Essa componente é dada por:
O momento a gente já calculou lá no passo 2 e vale:
A tensão vai ocorrer no eixo em torno do eixo então temos que ter o momento de inércia em relação à esse eixo:
Falta só o valor de , para isso a gente precisa olhar o perfil da nossa coluna :
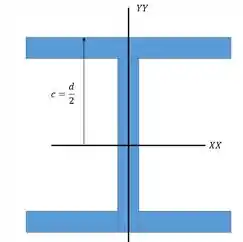
No caso desse tipo de perfil a gente vai ter quase sempre que é metade da altura . Para esse perfil temos que:
Assim,
Agora basta substituir na equação da tensão de flexão: