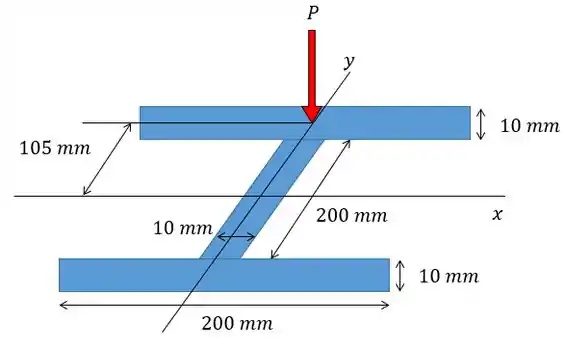
Uma coluna de de comprimento é feita de liga de alumínio . Se tiver presa por pinos no topo e na base e uma carga de compressão for aplicada no ponto , determine o valor permissível máximo de pelas equações da Seção 13.6 e pela equação 13.30.
Passo 1
Fala aí, pessoal!! Este problema pede para fazermos uma verificação de falhas da coluna através do método da tensão admissível (que é a equação 13.30 a qual o problema se refere) e tem o seguinte formato:
Para calcular essa tensão admissível nós vamos utilizar a tabela de equações para ligas de alumínio, que é dada pela :
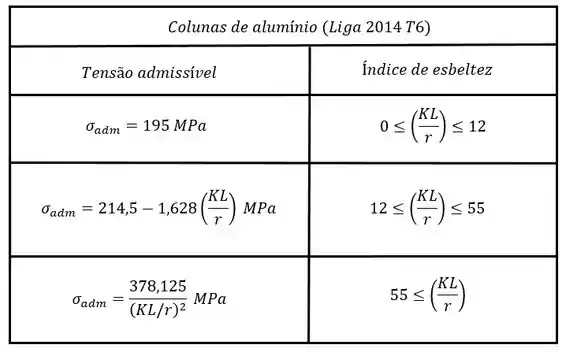
Então vamos calcular o índice de esbeltez, aplicar a equação correspondente e achar . Depois é só substituir na primeira equação e vamos ver se a coluna falha ou não =D
Passo 2
Para iniciar essa questão nós vamos calcular o momento de inércia da seção transversal, sua área e raio de giração:
Como nós temos três barras retangulares então vamos ter:
Agora podemos ir calculando o índice de esbeltez da coluna
Como a coluna está presa por pinos no topo e na base temos que , a altura da coluna é , agora falta achar o raio de giração , que pode ser achado através da relação entre o momento de inércia e a área.
A área é igual a:
Sendo assim vamos calcular o raio de giração com base no menor momento de inércia:
Logo, podemos calcular o valor do índice de esbeltez:
Passo 3
Utilizando esse valor para achar a equação correta da tabela vamos ter:
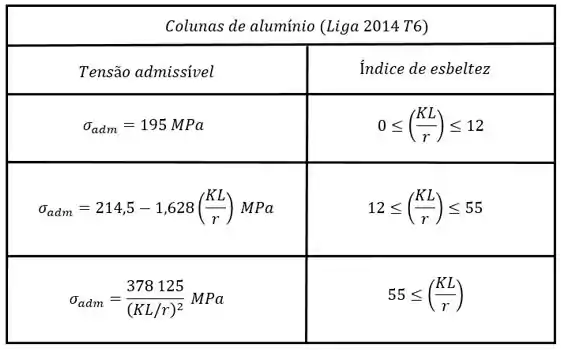
Logo vamos utilizar a equação:
Passo 4
Agora podemos aplicar a equação do método da tensão admissível.
Para a tensão de flexão vamos precisar do momento de inércia e da distância . Então a gente precisa lembrar que a flexão ocorre no eixo . Dessa forma vamos ter:
O resto dos valores nós já temos então vamos substituir na equação
Utilizando os dados em e vamos ter: