Deseja-se construir uma peça a fim de que a peça passe por um vão, o problema é que para que essa peça ultrapasse o vão é necessário que a mesma sofra uma redução de seção como mostra a figura. Sabendo que essa peça somente será sujeita a esforços de flexão discorra sobre os principais problemas encontrados nessa redução de seção.

Aqui temos que lembrar dos conceitos de concentração de tensão em flexão. Sabemos que sempre que mudamos bruscamente as seções entre peças ocorre o que chamamos de concentração de tensão. Essa concentração de tensão é contabilizada no que chamamos de coeficiente de concentração de tensão, que é obtido graficamente pelo seguinte gráfico

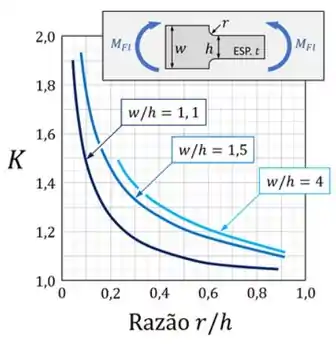
O que percebemos é que o coeficiente de concentração de tensões aumenta o valor das tensões médias que ocorrem na mudança de seção. Isso é altamente perigoso, pois suponha que a peça trabalhe em estados próximos do rompimento, se colocarmos ainda um fator de concentração de tensão, podemos acabar aumentando as tensões médias ao ponto de ultrapassarem a tensão admissível do material, se isso ocorresse poderia causar acidentes catastróficos dependendo de onde a peça fosse usada.

É muito importante tomar cuidado com isso, pois somente deve ser usado variação de seção em casos que não seja possível manter a seção constante.

Caso seja necessário variar a seção, que seja da forma mais suave possível, para evitar altas concentrações de tensões e consequentemente riscos de rompimento da peça.

Vale lembrar que a tensão máxima em concentrações de tensões devido a ação da flexão é dada por

Como pelo gráfico vemos que o valor de K só pode ser maior que 1, significa que sempre haverá aumento das tensões médias, sempre podendo levar a peça ao risco de rompimento pela variação da seção.