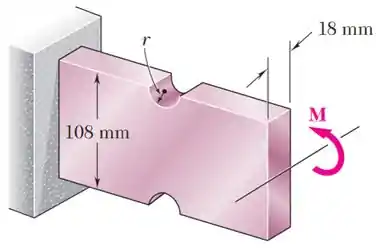
Ranhuras semicirculares de raio devem ser fresadas nos lados de uma barra de aço, conforme mostra a figura. Usando uma tensão admissível de , determine o maior momento fletor que pode ser aplicado ao elemento quando o raio das ranhuras semicirculares for e .
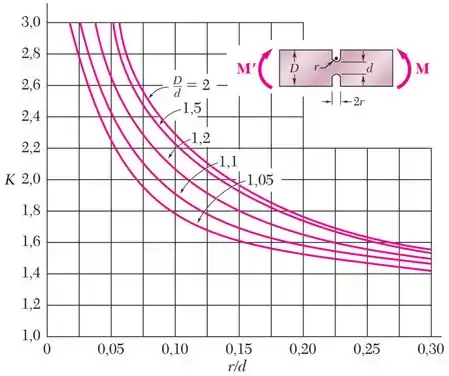
Para determinação do coeficiente de concentração de tensões , utilize o gráfico abaixo:
Passo 1
O que está acontecendo?
Devido ao momento fletor aplicado na peça da figura, vão surgir nas seções transversais dessa peça tensões de flexão de acordo com a fórmula da flexão:
Onde:
- (ou ) é o momento fletor na seção;
- é a posição do ponto em que se quer avaliar a tensão em relação à linha neutra da seção;
- & (ou ) é o momento de inércia da área da seção,
Agora...
Nesse caso do exercício, como todas as seções transversais dessa peça são retangulares, vamos ter que:
1. A linha neutra das seções dessa peça ficam bem no meio das seções:
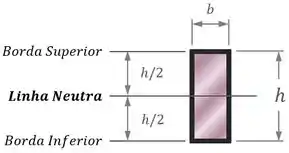
Dessa forma, os valores máximos da posição em relação à linha neutra (que implicam nos valores máximos da tensão ) são .
& 2. O momento de inércia da área das seções dessa peça vai ser dado pela fórmula:
Isso significa que a tensão máxima em uma seção dessa peça vai ser:
O que dá:
Ou, em módulo:
Daí que, vendo a nossa peça:
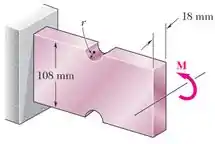
...vemos que as suas seções tem uma base e que tensão máxima na peça vai ocorrer para a seção com as ranhuras semicirculares, onde a altura vai ser:
O que é menor que a altura de das demais seções.
Agora, além disso...
Na seção das ranhuras nós ainda vamos ter um fator de concentração de tensões devido à mudança drástica de seção transversal causada pelas ranhuras.
Por causa desse fator, a tensão máxima na seção das ranhuras (que já é a seção de tensão máxima) deve ser multiplicada por um coeficiente de concentração de tensões .
Ou seja, para a nossa peça:
E o que é que o exercício quer?
Ele quer saber o momento fletor máximo que pode ser aplicado nessa peça de tal forma que as tensões na peça não superem a tensão admissível .
Ou seja, ele quer saber o momento fletor máximo que ainda satisfaz a condição:
Daí que, substituindo a expressão que acabamos de encontrar para :
...e isolando , vamos encontrar que esse momento fletor máximo vai ser dado por:
Aí, no item , o exercício quer que a gente determine esse momento fletor máximo considerando que as ranhuras tem um raio enquanto que no item devemos considerar .
Então, para resolver o exercício...
Devemos definir, para cada caso ( e ):
- A altura da seção transversal menor da peça;
- & o coeficiente de concentração de tensões , que pode ser obtido através do gráfico fornecido.
Feito isso, poderemos aplicar a fórmula que desenvolvemos acima:
...para cada situação, determinando assim o momento fletor máximo em cada caso, resolvendo o exercício.
Passo 2
Então vamos lá!
Começando pelo item :
Considerando que as ranhuras tem um raio , a seção menor da peça vai ter uma altura :
Definida essa altura, podemos definir em seguida o coeficiente de concentração de tensões para esse caso.
Para tanto, devemos olhar para o gráfico fornecido:
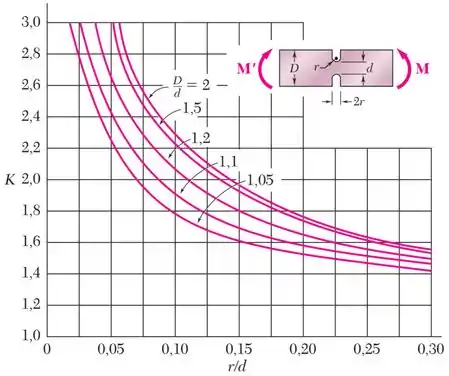
Olhando para o gráfico, vemos que temos que definir as razões e .
Daí que, olhando para o desenho em miniatura no canto do gráfico:
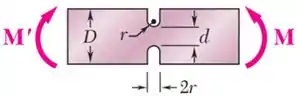
E comparando esse desenho com a nossa peça, identificamos que , e .
Dessa forma, conseguimos definir as razões:
Aí, inserindo esses valores no gráfico:
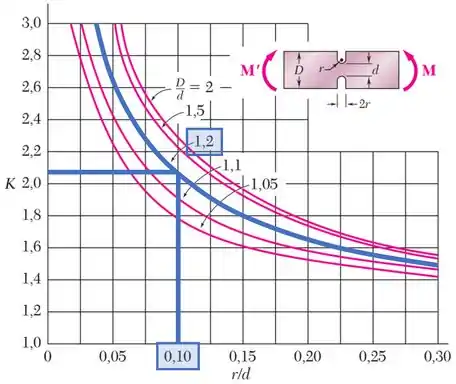
...encontramos que:
Passo 3
Agora que já definimos a altura e o coeficiente de concentração de tensões para o item , já podemos calcular o momento fletor máximo para esse item.
Aplicando a fórmula que desenvolvemos no passo , temos:
Substituindo:
- ;
- ;
- ;
- & ,
- ;
- ;
- ;
- & ,
Encontramos que:
Reescrevendo esse resultado em , temos:
O que significa que o momento fletor máximo permitido no caso em que é , que é a resposta do item .
Passo 4
Seguindo para o item :
Considerando que as ranhuras tem um raio , a seção menor da peça vai ter uma altura :
Em seguida, comparando com a nossa peça as dimensões indicadas no canto do gráfico de :
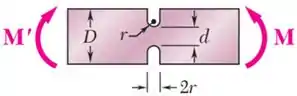
...encontramos que, no caso do item , , e .
Dessa forma, as razões e ficam assim:
Aí, inserindo os valores dessas razões no gráfico do coeficiente de concentração de tensões , de forma análoga ao que fizemos no passo , vamos encontrar que:
Passo 5
Por fim, só falta definir o momento fletor máximo para o item .
Aplicando a fórmula que desenvolvemos no passo , temos:
Substituindo:
Encontramos que:
Reescrevendo esse resultado em , temos:
O que significa que o momento fletor máximo permitido no caso em que é , que é a resposta do item .