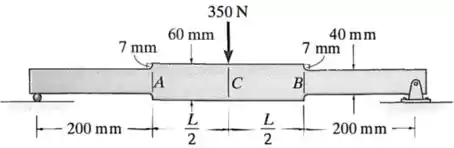
Determine o comprimento da porção da barra de modo que as tensões de flexão máximas em , e sejam as mesmas. A barra tem espessura de .
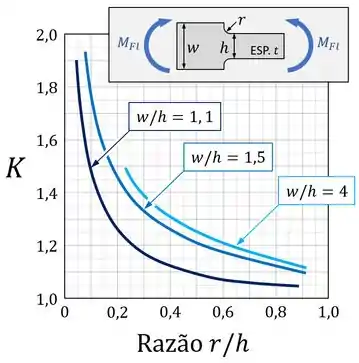
Para a determinação do coeficiente de concentração de tensões , utilize o gráfico abaixo:
Passo 1
O que está acontecendo?
Devido à carga aplicada na barra da figura, vão surgir esforços internos nela na forma de forças cortantes e momentos fletores .
Esses momentos fletores vão gerar tensões normais de flexão nas seções transversais da barra, de acordo com a fórmula da flexão:
Onde:
- (ou só “”) é o momento na seção;
- é a posição do ponto da seção em que se quer avaliar a tensão em relação à linha neutra de seção;
- & (ou só “”) é o momento de inércia da área da seção.
Sendo que aqui, como essa barra tem seções transversais sempre retangulares, vamos ter que:
1. O momento de inércia da área dessas seções vai ser dado pela fórmula:
Onde é a base da seção, igual à espessura de da barra para qualquer seção e é a altura da seção, igual à para as seções e e igual à para a seção .
(Dessa forma, temos que o momentos de inércia da área das seções e são iguais.)
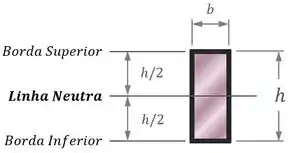
& 2. As tensões máximas nessas seções vão ocorrer nas bordas superiores e inferiores das seções, onde :
Além disso...
Nas seções e , devido à mudança brusca no tamanho da seção transversal, haverá uma concentração de tensões de acordo com um coeficiente , de tal forma que a tensão nessas seções vai ser dada por:
Sendo que o valor de pode ser encontrando utilizando o gráfico fornecido.
E, por fim...
Ainda temos que, como a carga é a única carga externa na barra e está centralizada entre os dois apoios na barra, os esforços externos e internos nessa barra vão ser simétricos.
Dessa forma, vamos ter que o momento fletor nos pontos e vão ser iguais.
E o que é que o exercício quer?
Ele quer saber qual deve ser o comprimento indicado na figura para que as tensões de flexão máximas no ponto , que ocorrem nos pontos :
Seja igual às tensões de flexão máximas nos pontos e , que ocorrem nos pontos , e onde há uma concentração de tensões
Então, para resolver o exercício…
Temos que:
1. Aplicar os métodos da estática (DCL, equilíbrio, análise dos esforços internos) para descobrir os momentos fletores em e (que vão ser iguais) e em , em função do comprimento ;
2. Determinar o coeficiente de concentração de tensões nos pontos e ;
& 3. Igualar as tensões máximas e acima e isolar o comprimento , descobrindo assim qual o valor desse comprimento para que essas tensões sejam iguais.
Passo 2
Então vamos começar fazendo o diagrama de corpo livre ou “DCL” da peça!
Nela, temos:
- No ponto “” na extremidade esquerda da barra, um apoio móvel que vai realizar uma reação na vertical ;
- E no ponto “” na extremidade direita, um apoio fixo que vai realizar uma reação na horizontal (que vai acabar sendo nula e pode ser omitida do DCL) e uma reação na vertical .
Dessa forma, o nosso DCL fica assim:
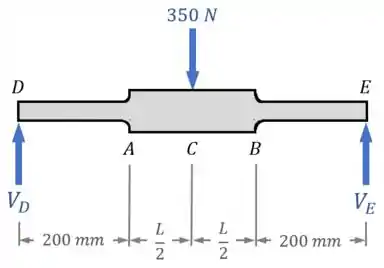
Passo 3
Feito o DCL, podemos aplicar o equilíbrio na peça.
Aplicando o somatório de forças na vertical, temos:
O que significa que:
E aplicando o somatório de momentos em relação ao ponto , temos:
Dividindo tudo por e isolando , encontramos que:
Aí, substituindo essa relação que encontramos na expressão anterior , encontramos que:
O que significa que:
E, como , isso significa que:
E assim terminamos de determinar todos os esforços externos na nossa peça.
Passo 4
Em seguida, fazemos uma análise dos esforços internos.
Aqui, nosso objetivo é descobrir os momentos fletores em , e .
Mas como já sabemos que o momento fletor em é igual ao em , só precisamos determinar os momentos fletores em e em .
Dessa forma, sabendo que as mudanças na seção transversal não afetam os esforços internos, é suficiente observar os esforços internos somente nas seções entre e :
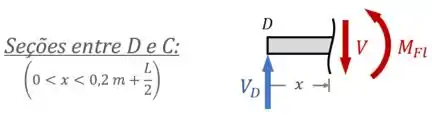
...para determinarmos os momentos fletores em e em .
Aí, aplicando o equilíbrio de momentos para o desenho acima em relação ao ponto da seção, temos:
Substituindo e isolando , encontramos que:
Aí, como para o ponto , , temos que:
E como para o ponto , , temos:
Passo 5
Agora, antes de prosseguir com a resolução do exercício, precisamos determinar o coeficiente de concentração de tensões em e .
Então vamos olhar para o gráfico de :
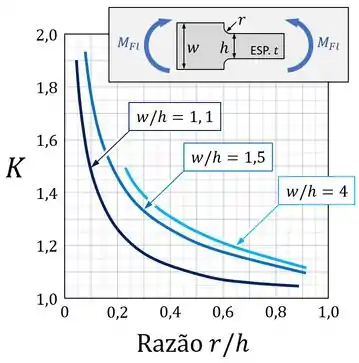
Comparando as medidas indicadas no esquema no topo dessa gráfico com as medidas indicadas na figura original do exercício, vemos que , e .
Assim, podemos calcular as razões:
Aí, escolhendo a curva para e inserindo o valor da razão no gráfico acima, encontramos que:
Passo 6
Agora que já:
- Usamos o que precisávamos dos métodos da estática para determinar os momentos fletores em e , e em , ;
- E determinamos o coeficiente de concentração de tensões em e ,
...podemos seguir para a próxima etapa do exercício.
O exercício quer saber qual o comprimento para o qual as tensões máximas em , e são iguais.
Então vamos igualar essas tensões:
Aplicando a fórmula da flexão para a determinação das tensões máximas nesses pontos, e lembrando da concentração de tensões nos pontos e , vamos ter que:
Simplificando, isso fica assim:
Aplicando a formula do momento de inércia da área de um elemento retangular para cada seção, vamos ter:
Simplificando tudo que é possível simplificar, temos:
Em seguida, substituímos os valores encontrados no passo anterior para e :
Multiplicando tudo por , temos:
Aí, fazendo a distributiva do lado esquerdo:
Passando para o outro lado e colocando em evidência:
E isolando , encontramos que:
Por fim, substituindo:
- ;
- ;
- & ,
Encontramos que: