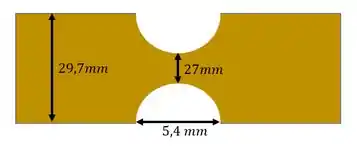
A peça de seção variável abaixo sofre a ação de um esforço fletor. Sabendo que a mesma possui resistência máxima a ação do normal de , determine o máximo momento ao qual podemos submeter essa peça sem que ela rompa.
Passo 1
Aqui nos temos que tomar o seguinte cuidado, vamos fazer o processo contrario do que estamos acostumados, primeiro vamos determinar os valores da nossa fórmula final e depois vamos abrindo cada parte da nossa fórmula.
A nossa fórmula final será a seguinte
Sabemos pelo enunciado que
Precisamos determinar o valor de K graficamente e só com isso já conseguimos determinar o valor de tensão média, então vamos lá.
Passo 2
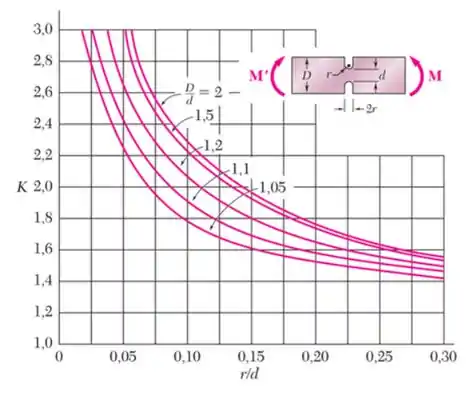
Para determinar o valor do K precisamos seguir alguns planejamentos, primeiro vamos determinar a melhor curva pela relação
Em que cada letra está relacionada com a nossa peça pela imagem abaixo
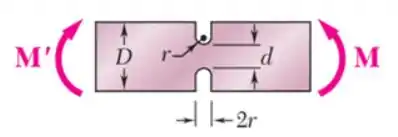
Sabemos que pela nossa peça esses valores são
substituindo
Agora que já temos a melhor curva precisamos do valor horizontal, e para determinarmos esse valor usamos a relação
Em que
Já determinamos a melhor curva e o valor horizontal, agora só falta determinar o valor de K, que obtemos graficamente
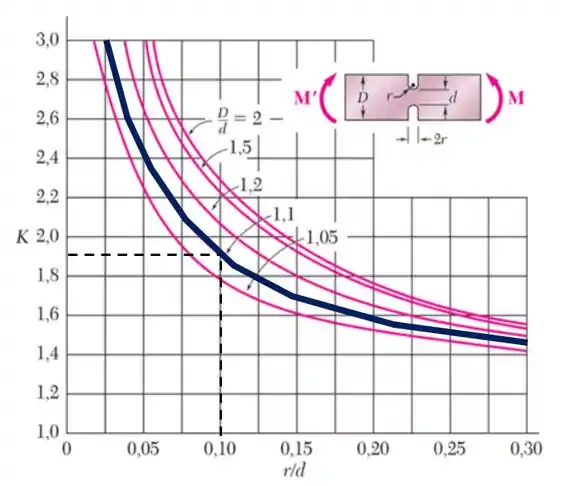
Logo o valor de K será
Passo 3
Calculado esses dois valores vamos determinar a tensão média
Sabemos que a tensão média é calculada pela forma da flexão, então podemos escreve-la como
Substituindo na nossa equação os valores que já temos
Agora vem a grande pergunta, qual seção usar? a maior ou a menor?
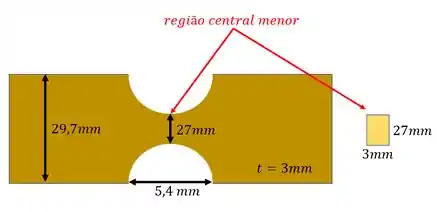
Queremos maximizar a tensão, logo usamos a menor seção, pois quanto menor o momento de inercia, maior o valor da tensão, que é exatamente o que queremos. A menor seção é retangular com dimensões (3x27) mm, logo a fórmula para fazer os cálculos são
Sabemos que as dimensões são
Em que Y é a metade da altura da menor seção
Substituindo os valores teremos que