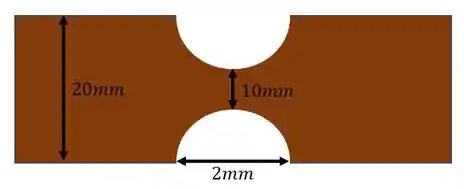
Para a peça de madeira abaixo com seção retangular de espessura 7mm determine a maior tensão normal que ela será submetida caso seja sujeita a um momento fletor de .
Passo 1
Pra resolver esse exercício vamos dividir a solução em 3 partes. A primeira parte será definir o valor da tensão média pela fórmula
Em que
Aqui vale lembrar que usamos os valores da menor seção pois é nela que ocorrerá a maior tensão média, sempre lembre disso, usar os dados da menor seção, só usamos os valores da maior seção para definirmos o valor do coeficiente de concentração.
A segunda parte da nossa solução se trata de acharmos o coeficiente de concentração de tensão e para fazermos isso precisaremos de 3 coisas.
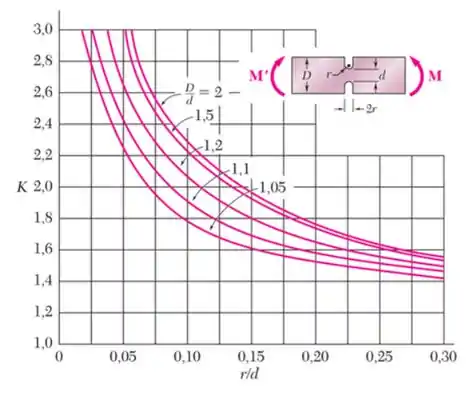
- Primeiro usar um gráfico para determinar o coeficiente de concentração de tensão
- Segundo devemos determinar qual a melhor curva do nosso gráfico para resolver o problema, e para isso usamos a relação
Em que no nosso caso se trata da relação entre as alturas da nossa peça como mostra a figura
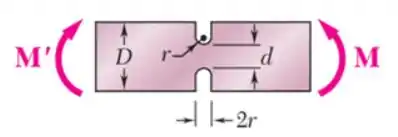
- E por fim a terceira parte se trata de encontrarmos o valor no eixo horizontal do nosso gráfico, que encontraremos pela relação
Por fim a terceira parte da nossa solução será relacionar a tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula
Passo 2
Agora que já sabemos como calcular cada termo vamos a prática.
Como vimos a primeira parte da solução se trata de calcularmos a tensão cisalhante média pela fórmula
Em que sabemos que a menor seção é dada pela região central
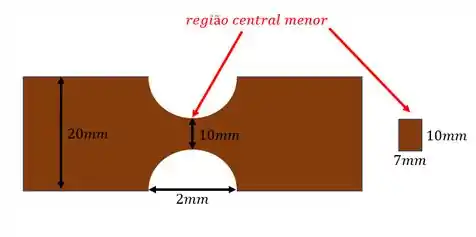
E para a tensão média temos que
Passo 3
Vamos agora determinar o coeficiente de concentração de tensão.
Sabemos que primeiro devemos usar um gráfico, que é esse aqui
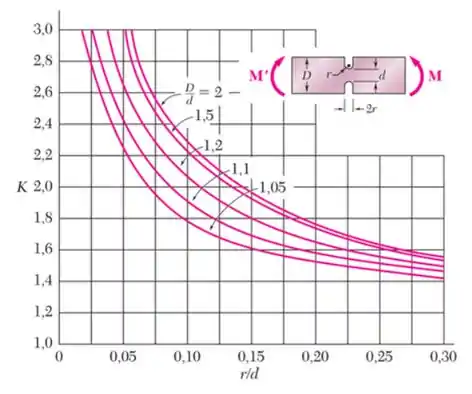
Depois devemos determinar a melhor curva pela relação
Agora que já sabemos a melhor curva só falta determinar o valor horizontal, que determinamos pela fórmula
Agora vamos determinar o valor do K
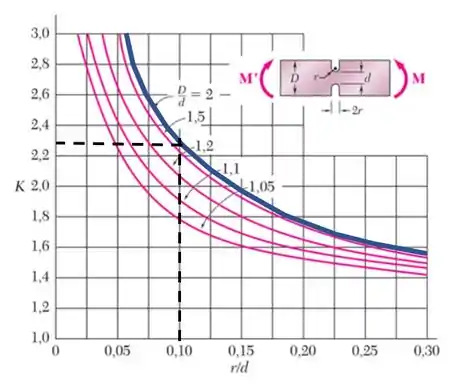
Passo 4
Agora basta relacionarmos a nossa tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula