Considere uma embalagem de maçãs, cada uma com de diâmetro, na qual o ar escoa a e com velocidade de . O valor do coeficiente de transferência de calor por convecção é . No interior de cada maçã, a energia térmica é gerada uniformemente a uma taxa total de . A massa específica e a condutividade térmica da maçã são respectivamente e .
Determine as temperaturas do centro e da superfície da maçã.
Passo 1
Bora dar uma olhada num esquema que representa esse problema:
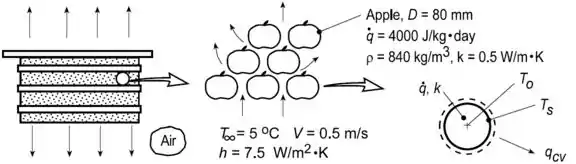
Como nosso objetivo é calcular a temperatura no centro e na superfície das maçãs e elas podem ser aproximadas de esferas, vamos usar a equação do calor em coordenadas esféricas:
Ao admitir que a condução é adimensional na direção e que as propriedades são constantes, considerando no regime estacionário, ficamos com:
Reorganizando a equação:
Integrando em termos do raio :
Reorganizando:
Integrando novamente:
Pronto! Conseguimos determinar o perfil de temperatura! Agora só a gente achar as constantes pelas condições de contorno.
Passo 2
Vamos avaliar a situação pra definir quais serão as condições de contorno:
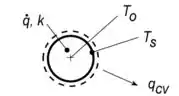
A primeira condição de contorno que usaremos tem a ver com a simetria da esfera. “Como assim?”
Você pode pensar de duas formas diferentes:
- A energia que é gerada no volume da esfera acaba saindo por convecção pra todos os lados, devido à simetria do corpo. Sendo assim, o fluxo de calor no centro da esfera é zero.
- Como a energia é gerada em todo o volume e sai pelas superfícies, a gente pode esperar que o centro seja o ponto de máxima temperatura da esfera. Sendo assim, a derivada da temperatura no centro é zero.
Então, bora lá:
- Condição de contorno 1: fluxo de calor zero no centro.
Já encontramos no Passo 1, a expressão da derivada da temperatura:
Note que, ao avaliarmos a equação na posição , o termo com a constante tende ao infinito. Como a derivada não pode tender ao infinito, a constante deve ser zero pra cancelar a contribuição desse termo:
Passo 3
Além disso, as maçãs estão suscetíveis a convecção do ar que escoa sobre elas, logo a condição de contorno em é de convecção na superfície. Dá uma olhada:
- Condição de contorno 2: convecção na superfície.
Substituindo a expressão da derivada da temperatura avaliada em , ficamos com:
Logo:
Antes de substituir os valores, bora converter a taxa volumétrica () pra unidade no SI:
Substituindo os valores do enunciado e a taxa convertida em SI:
Em graus Celcius:
Passo 4
Agora a gente só precisa determinar a temperatura do centro! Avaliando o perfil de temperatura no centro:
Logo:
Avaliando o perfil em na superfície:
Assim, isolando a temperartuta do centro ():
Substituindo os valores:
Em graus Celcius: