Um proprietário de um imóvel, cuja tubulação de água congelou durante um período de tempo frio, decide derreter o gelo passando uma corrente elétrica ao longo da parede do tubo. Os raios interno e externo são designados por e , e sua resistência elétrica por unidade de comprimento por . O tubo é bem isolado no exterior e durante a fusão do gelo (e água) permanece a uma temperatura constante no tubo associada ao processo de fusão.
Considerando que condições de regime estacionário são alcançadas logo depois da aplicação da corrente, determine a forma de distribuição de temperatura em regime estacionário na parede do tubo durante o processo de fusão.
Desenvolva uma expressão para o tempo necessário para fundir totalmente o gelo. Calcule esse tempo para , e .
Passo 1
Considerando que condições de regime estacionário são alcançadas logo depois da aplicação da corrente, determine a forma de distribuição de temperatura em regime estacionário na parede do tubo durante o processo de fusão.
Vamos antes de iniciar o problema, identificar todos os dados do enunciado: , , , , e . Beleza, então já sabemos que o perfil de temperatura solicitado deve estar em função somente desses parâmetros!
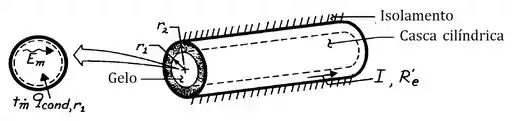
Como queremos determinar o perfil de temperatura em uma casca cilíndrica, vamos recorrer à equação do calor em coordenadas cilíndricas:
Ao admitir que a condução de calor é unidimensional em e as propriedades são constantes, temos que:
Pelo enunciado, as condições de regime estacionário são alcançadas instantaneamente, então, não há variação da temperatura ao longo do tempo. Assim:
Reorganizando a equação, a gente fica com:
Integrando a equação em termos de :
Reorganizando essa equação:
Integrando novamente a equação em termo de , a gente fica com:
Pronto! Esse é o perfil de temperatura num corpo cilíndrico. Mas repara que a gente não usou nenhum dos dados ainda! Isso porque a gente ainda não determinou as constantes e .
Passo 2
Pra gente determinar as constantes, precisamos das famosas condições de contorno. Pra identificar quais são as condições de contorno desse problema, dá uma olhadinha no esquema de novo aqui embaixo:
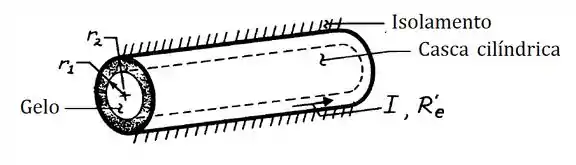
Pela imagem, a gente pode perceber que na superfície em , o fluxo de calor é zero, devido ao isolamento, então a condição de contorno será de fluxo constante nulo. Já em , a superfície está em contato com o gelo (), logo a condição de contorno será de temperatura constante e igual a .
Vamos trabalhar com uma condição por vez, beleza?
Passo 3
Bora usar essas condições de contorno agora:
- Condição de contorno 1: fluxo zero na parede em .
- Condição de contorno 2: temperatura constante e igual a .
Já encontramos no Passo 1, a expressão da derivada da temperatura:
Substituindo na equação:
Reorganizando a equação:
Passo 4
Substituindo na expressão do perfil que encontramos no Passo 1:
Então, ficamos com:
Avaliando em e substituindo o valor encontrado anteriormente de :
Passo 4
Pronto! Encontramos as duas constantes! Agora é só substituir na expressão do perfil de temperatura:
Reorganizando essa bagunça de letras, a gente fica com:
Esse é o perfil de temperatura na casca cilíndrica! Mas tem um detalhe: ele não tá escrito somente em termos daqueles parâmetros que mencionamos (, , , , e ). O calor gerado () não pode estar na expressão do perfil.
Passo 5
Pra solucionar esse problema, a gente vai tentar escrever ele em função dos demais parâmetros!
A gente sabe que a energia que é gerada é uma consequência do efeito Joule, ou seja, a corrente elétrica que passa dissipa uma taxa volumétrica de calor. E sabemos que a taxa de energia pode ser escrita como:
Assim:
Mas o dado é em termos de , ou seja, é a resistência por unidade de comprimento:
Em que é o comprimento da casca cilíndrica e é seu volume.
Em que essa área é a área transversal da casca cilíndrica:

Dessa maneira:
Substituindo as expressões:
Passo 6
Desenvolva uma expressão para o tempo necessário para fundir totalmente o gelo. Calcule esse tempo para , e .
Fazendo um balanço de energia no corpo de gelo, a gente fica com:
Dividindo pela unidade de comprimento , ficamos com:
Substituindo a expressão da taxa de calor volumétrica:
Com os valores do enunciado, temos que:
Resposta