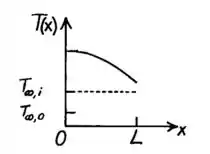
O ar no interior de uma câmara a é aquecido por convecção com por uma parede de espessura de e condutividade térmica com geração uniforme de calor de . Para evitar que a geração de calor no interior da parede seja perdida para o exterior da câmara a com , um aquecedor elétrico de fita é colocado na rede externa para fornecer um fluxo uniforme de calor .
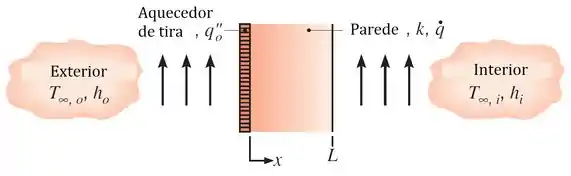
Esboce a distribuição de temperatura na parede em coordenadas para a condição em que não ocorre a perda do calor gerado no interior da parede para o exterior da câmara.
Quais são as temperaturas nas fronteiras da parede ( e ), para as condições do item ?
Determine o valor de que deve ser fornecido pelo aquecedor de fita de modo qe todo o calor gerado no interior da parede seja transferido para o interior da câmara.
Se a geração de calor da parede for interrompida e o fluxo de calor do aquecedor de fita mantido constante, qual seria a temperatura em regime estacionário da superfície externa da parede?
Passo 1
Esboce a distribuição de temperatura na parede em coordenadas para a condição em que não ocorre a perda do calor gerado no interior da parede para o exterior da câmara.
Nosso objetivo aqui é construir o perfil de temperatura dentro da parede com geração. Para isso, temos que recorrer à equação do calor em sistemas cartesianos:
Ao admitir a condução somente na direção e propriedades constantes, avaliando o estado estacionário, ficamos com:
Reorganizando a equação:
Assim, podemos integrar a equação em relação a :
Integrando mais uma vez a equação em termos de :
Assim, temos que o perfil de temperaturas é dado por:
Logo, verificamos que o perfil de temperatura é parabólico! Para saber exatamente como ele é, a gente precisa das condições de contorno! Mas de forma qualitativa, a gente pode avaliar o seguinte:
A função é um semi-parábola, porque em não há perdas de energia para o ambiente, porque um fluxo de calor é fornecido nesse ponto de mesmo valor que seria a perda de energia por convecção.
Concluímos que a derivada da temperatura é zero em e, consequentemente, esse é um ponto de máximo ou de mínimo.
Como um fluxo de calor é fornecido na superfície em , espera-se que essa superfície seja mais quente que a de , logo é um ponto de máximo!
Então, o perfil será:
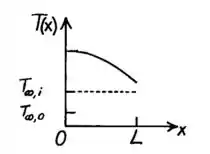
Passo 2
Quais são as temperaturas nas fronteiras da parede e , para as condições do item ?
Temos agora que determinar quais as temperaturas da parede: e . Como já vimos na letra a), o perfil de temperaturas dentro da parede é dado por:
Então, se conseguirmos descobrir as constantes e , poderemos calcular a temperatura em qualquer posição de , inclusive nas extremidades como é o nosso objetivo!
Para isso, a gente precisa de condições de contorno! Vamos avaliar quais são as condições de contorno. O sistema é o seguinte:
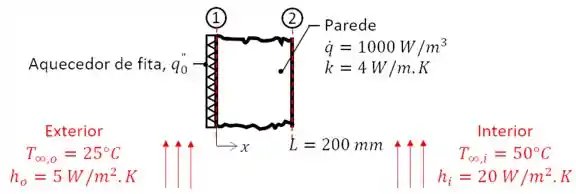
Note que, na superfície , temos a condição de um fluxo zero () e, na superfície , temos a condição do fluxo de condução ser igual ao de convecção. Então vamos trabalhar com cada condição separadamente.
Passo 3
Condição de contorno 1: fluxo zero na parede.
Já sabemos a expressão para a derivada da temperatura na letra a):
Em , temos:
Substituindo na equação:
Passo 4
Condição de contorno 2: fluxo de condução igual ao de convecção.
Substituindo a expressão da derivada da temperatura avaliada em , ficamos com:
Já sabemos que , então:
Logo:
Substituindo os valores:
Já achamos a temperatura de uma das extremidades só com essa condição de contorno! Show!
Passo 5
Se a gente avaliar o perfil em , ficaremos com:
Logo, concluímos que:
Avaliando o perfil de temperatura em , ficamos com:
Substituindo os valores:
Assim:
Passo 6
Determine o valor de que deve ser fornecido pelo aquecedor de fita de modo que todo o calor gerado no interior da parede seja transferido para o interior da câmara.
O aquecedor de tira deve fornecer um fluxo de calor suficiente para que a perda de calor para o exterior seja zero, ou seja, a quantidade de calor que ele fornece deve ser igual ao fluxo de calor que seria perdido por convecção:
Sendo assim, vamos calcular o calor de convecção que seria perdido se não houvesse o aquecedor:
Substituindo os valores:
Passo 7
Se a geração de calor da parede for interrompida e o fluxo de calor do aquecedor de fita mantido constante, qual seria a temperatura em regime estacionário da superfície externa da parede?
Se a geração de calor for interrompida a gente cai nas situações que já vimos nos outros tópicos: condução sem geração.
Sendo assim, a gente pode usar circuito térmico em todo o sistema! Dá uma olhadinha:
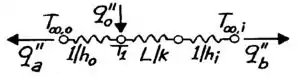
Fazendo um balanço de energia no nó de temperatura , a gente fica com:
Substituindo as expressões com as resistências térmicas:
Substituindo os valores de cada propriedade:
Reorganizando os termos, temos que:
Resposta