Uma parede plana é composta por dois materiais e. A parede de material apresenta uma geração de energia de , e espessura de . A parede de material , sem geração de calor, é caracterizada por e .
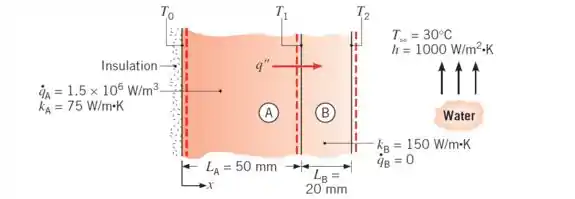
A superfície interna do material é bem isolada, enquanto que a superfície externa está sendo resfriada por uma corrente de água a e .
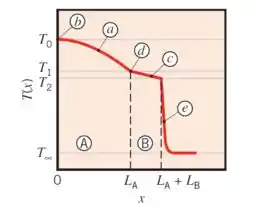
Esquematize o perfil de temperatura que existe no sistema sob condições de estado estacionário.
Determine a temperatura da interface dos materiais e a temperatura da superfície resfriada.
Passo 1
Esquematize o perfil de temperatura que existe no sistema sob condições de estado estacionário.
Já discutimos nos tópicos anteriores como são os perfis de temperatura na parede plana com geração (parabólico) e sem geração (reta). Então vamos analisar como o perfil de temperatura se comporta em cada material.
Material A:
Além disso, sabemos que o fluxo de calor na superfície isolada é zero, ou seja:
Se a derivada da temperatura é nula, isso significa que esse ponto será um ponto de máxima ou de mínima temperatura.
Como há geração de calor na superfície A e esse calor só escapa pela direita (lado do material B), podemos afirmar que:
Sendo assim, a gente conclui que a temperatura em é um ponto de máximo e a parábola no material tem concavidade pra baixo!
Passo 2
Material B:
Por fim, a gente pode avaliar a derivada das curvas na transição do material A para o material . “Mas como?”
A condutividade térmica nos dá essa informação! Quanto maior a condutividade térmica de um material, menor será a resistência térmica de condução e, consequentemente, as temperaturas estre duas extremidades serão mais parecidas.
Sendo assim, quando a gente avalia quantos graus variaram em um determinado espaço de tempo (conceito da derivada), esse valor será pequeno.
Sendo assim, como a condutividade térmica do material é maior que a do material , podemos afirmar que a derivada do perfil em será menor que a derivada em .
Passo 3
Por fim, o perfil de temperatura da superfície para o fluido é semelhante a uma exponencial, pois a convecção é um fenômeno muito intenso e a temperatura, em pouco espaço, já alcança o valor da temperatura no seio do fluido ().
Diante disso tudo, propomos o seguinte perfil de temperatura:
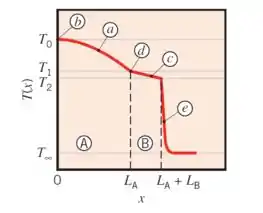
Passo 4
Determine a temperatura da interface dos materiais e a temperatura da superfície resfriada.
A temperatura da superfície externa () pode ser obtida se fizermos um balanço de energia na parede de material . Como não há geração nesse material, temos que o fluxo de calor que entra pela superfície a temperatura de é o mesmo fluxo que sai por convecção pela superfície a :
Esse fluxo de calor pode ser determinado por um segundo balanço de energia, mas agora na parede de material . Como não há fluxo pela superfícies isolada, todo o calor gerado no material , sai pela superfície em .
Dessa maneira, a gente pode escrever o seguinte:
Dividindo pela área de troca térmica, pra escrevermos em termos do fluxo de calor e não da taxa, ficamos com:
Igualando as duas expressões pro fluxo que achamos, teremos:
Isolando a temperatura , a gente fica com:
Onde:
Substituindo os valores:
Passo 5
Pra gente encontrar a temperatura , a gente pode fazer um circuito na parte da direita do sistema, porque ali não há geração então a gente pode montar circuito térmico!
Fazendo isso, teremos o seguinte:

Dessa maneira a gente pode escrever o fluxo de calor da seguinte forma:
Obs.: Estamso definindo as resistências térmicas associadas ao fluxo de calor, ao invés da taxa de transferência de calor.
Isolando a temperatura de interesse , a gente tem que:
Onde:
Substituindo os valores:
Resposta
O perfil de temperatura no sistema é dado abaixo: