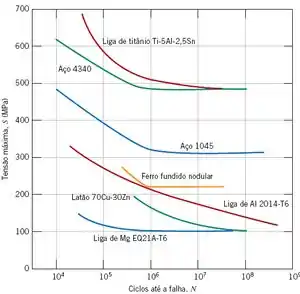
Uma barra cilíndrica com 14,7 mm de diâmetro, fabricada a partir de uma liga de titânio Ti-5Al-2,5Sn (Figura abaixo), é submetida a um ciclo de aplicação de cargas repetidas de tração e de compressão ao longo do seu eixo. Calcule as cargas máxima e mínima que deverão ser aplicadas para produzir uma vida em fadiga de ciclos. Assuma que os dados na Figura abaixo tenham sido tomados a partir de ensaios com cargas axiais repetidas de tração e de compressão, que a tensão indicada no eixo vertical seja a amplitude de tensão, e que os dados tenham sido obtidos para uma tensão média de 50 MPa.
Passo 1
Observando a curva S-N acima para o ciclos até nota-se que a tensão máxima que nossa barra poderá sofrer, é de, aproximadamente, .
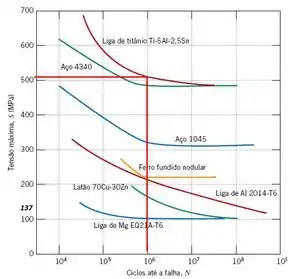
Para calcularmos a tensão e um componente sob tensões axiais utilizamos a formula abaixo:
Em que é a força aplicada no ensaio e A é a área do corpo de prova.
Além da tensão máxima, obtida através do gráfico, o problema nos dá:
Passo 2
Agora vamos obter os valores das cargas máximas e mínimas para isso vamos calcular as tensões máxima e mínima:
Passo 3
Sabemos que:
Assim, as cargas são: