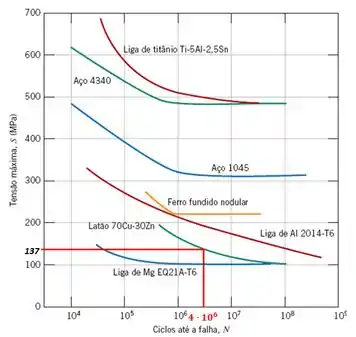
Uma barra cilíndrica com 6,7 mm de diâmetro, fabricada a partir de uma liga de latão 70Cu-30Zn, é submetida a um ciclo de aplicação de cargas giratórias com dobramento; os resultados dos ensaios (na forma do comportamento S-N) estão mostrados na Figura abaixo. Se as cargas máxima e mínima são de +120 N e –120 N, respectivamente, determine a sua vida em fadiga. Considere que a distância de separação entre os pontos de suporte da carga seja de 67,5 mm.
Passo 1
O problema nos fornece os seguintes dados:
Através da formula de flexão vamos calcular as tensões máxima e mínima(Obs.: Se deixarmos a força em e as medidas em obteremos a tensão em :
Passo 2
Vamos agora calcular a tensão alternada. Precisamos dessa tensão pois a curva S-N foi obtida através de ciclos de tensões alternadas. Outra coisa que temos que está atento e que o eixo , ciclos até a falha, , está em escala logarítmica.
Repare que quando tivermos forças ou tensões máximas e mínimas igual em modulo a tensão alternada é:
Como dito a tensão máxima está em função do logaritmo do número de ciclos até a falha por fadiga (), assim, traçado um reta na tensão até chegar na curva S-N do material, teremos o seguinte número de ciclos até a falha por fadiga: