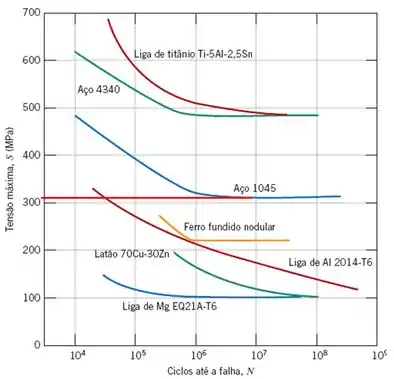
Uma barra cilíndrica, de aço 1045, que tem comportamento S-N conforme está apresentado na Figura abaixo, é submetida a ensaios giratórios com dobramento segundo ciclos alternados de tensões. Se o diâmetro da barra é de 15,0 mm, determine a carga cíclica máxima que pode ser aplicada para assegurar que não irá ocorrer uma falha por fadiga. Considere um fator de segurança de 2,0 e que a distância entre os pontos de aplicação de carga seja de 60,0 mm (0,0600 m).
Passo 1
Observando a curva S-N acima nota-se que o limite de resistência à fadiga, portanto a tensão máxima que nossa barra poderá sofrer, é de, aproximadamente, .
Para calcularmos a tensão máxima e um componente sob flexão utilizamos a formula da flexão para barra redonda:
Em que é a força aplicada no ensaio, é o comprimento do corpo de prova e é o diâmetro do corpo de prova.
Além da tensão máxima, obtida através do gráfico, o problema nos dá:
Como o problema nos fornece o fato de segurança devemos dividir nossa tensão máxima por esse fator, assim:
Isolando a força na equação acima teremos (Obs.: Se deixarmos a tensão em e as medidas em obteremos a força em :