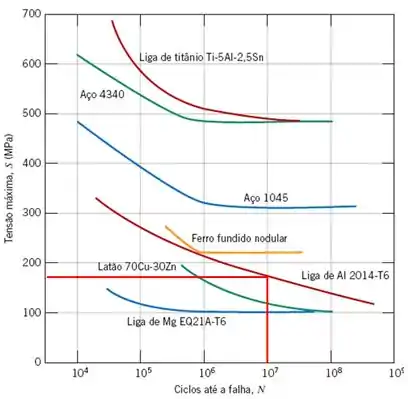
Uma barra cilíndrica em liga de alumínio 2014-T6 é submetida a um ciclo de tensões de tração e de compressão ao longo do seu eixo; os resultados desses testes estão mostrados na Figura abaixo. Se o diâmetro da barra é de 12,0 mm, calcule a amplitude de carga máxima permissível (em N) para assegurar que não ocorrerá uma falha por fadiga em ciclos. Assuma um fator de segurança de 3,0, que os dados na Figura abaixo foram tomados a partir de ensaios alternados axiais de tração e de compressão, e que T seja a amplitude da tensão.
Passo 1
Observando a curva S-N acima para o ciclos até nota-se que a tensão máxima que nossa barra poderá sofrer, é de, aproximadamente, , suponha que seja um carregamento com ciclo mínimo nulo:
Para calcularmos a tensão máxima e um componente sob tensões axiais utilizamos a formula abaixo:
Em que é a força aplicada no ensaio e A é a área do corpo de prova.
Além da tensão máxima, obtida através do gráfico, o problema nos dá:
Como o problema nos fornece o fato de segurança devemos dividir nossa tensão máxima por esse fator, assim:
Isolando a força na equação acima teremos (Obs.: Se deixarmos a tensão em e as medidas em obteremos a força em :
Logo, a carga máxima permissível (em N) para assegurar que não ocorrerá uma falha por fadiga em ciclos é de: