Uma esfera condutora de raio está no interior de uma casca esférica fina condutora de raio . A esfera e a casca esférica são concêntricas e o espaço entre elas está preenchido com
um material de condutividade constante, ( é uma constante positiva). Uma
corrente elétrica , uniformemente distribuída através do material entre os condutores, flui da esfera interna para a casca esférica.
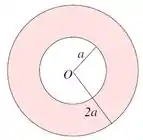
- Determine a dimensão da constante no Sistema Internacional de Unidades.
- Calcule a resistência elétrica entre os condutores.
- Dada uma diferença de potencial aplicada entre as duas superfícies, calcule o vetor densidade de corrente em função dos dados do problema.
Passo 1
a)O enunciado disse pra gente que a condutividade é dada por . Vamos lembrar que a condutividade de um material tem unidade de inverso de resistência multiplicado pelo inverso de unidade de comprimento e que é uma unidade de comprimento, então:
Então, tem unidade do inverso de Ohm.
Passo 2
b)A gente pode considerar que a camada entre os dois condutores é infinitesimal com espessura . Vamos lembrar também que a superfície de uma esfera tem área .
Então podemos calcular a resistência dessa camada pela expressão:
Que substituindo , também pode ser escrita como:
Integrando de até , temos que
Então, a nossa resistência vai ser
Passo 3
c)A diferença de potencial aplicada vai gerar uma corrente certo? A gente pode escrever essa corrente isolando o na Lei de Ohm:
Do item b, nós sabemos qual a expressão para , vamos substituir então
Por conservação de carga, devemos ter para qualquer superfície fechada passando entre e .
Vamos então considerar, usando simetria radial, uma superfície esférica de raio :
Mas ali em cima a gente também calculou que
Então vamos igualar as duas expressões
Então, a nossa densidade de carga vai ser:
Resposta
- Ohm.