O filamento incandescente (de diâmetro ) de uma lâmpada é conectado a dois fios mais espessos de diâmetro .
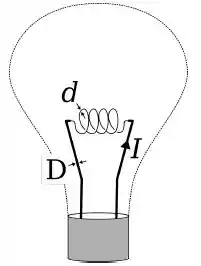
Sabendo que quando a lâmpada está acesa a densidade de corrente no fio de diâmetro vale , a densidade de corrente no filamento vale:
Passo 1
Como a corrente é constante tanto no fio de diâmetro , quanto no de diâmetro , temos que:
Onde, para um fio cilíndrico de diâmetro , a área é dada por:
Logo:
Passo 2
Substituindo os valores, teremos:
Resposta
Exercícios de Livros Relacionados
Um fio de cobre de calibre 10 conduz uma corrente de 20A . Considerando que o cobre tenha um elétron livre por átomo, calcule a rapidez de deriva dos elétrons livres no fio.
Uma corrente pequena, porém mensurável, de 1,2 × 10 - 10 A atravessa um fio de cobre de 2,5 m m de diâmetro. O número de portadores de carga por unidade de volume é 8,49 × 10 28 m - 3 . Supondo que a
O fusível de um circuito elétrico é um fio projetado para fundir, abrindo o circuito, se a corrente ultrapassar um certo valor. Suponha que o material a ser usado em um fusível funda quando a densidad
Um pedaço de fio de cobre calibre 10 e um pedaço de fio de cobre calibre 14 estão soldados entre si nas duas extremidades. Os fios conduzem uma corrente de 15A . (a) Se há um elétron livre para cada á
Em um dos feixes que colidem em um supercolisor de prótons, os prótons estão se movendo com velocidades aproximadamente iguais à velocidade da luz e a corrente do feixe é 5,00m A . A densidade de corr