(II) A figura abaixo mostra a seção reta de uma casca cilíndrica muito longa de raio interno e raio externo , coaxial com o eixo . Pela casca flui, na direção positiva do eixo (direção saindo do papel), uma corrente uniformemente distribuída através de sua seção reta.
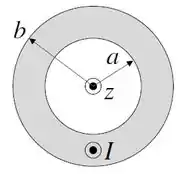
(a) (0,5 ponto) Calcule o vetor densidade de corrente na região , onde é a distância ao eixo da casca cilíndrica.
(b) (1,0 ponto) Calcule o vetor campo magnético na região .
Passo 1
Por definição, densidade de corrente é a corrente que flui por unidade de área da seção reta.
Vamos começar, então, calculando esta área , que nada mais é do que a área da seção reta da casca cilíndrica. Temos:
Passo 2
Calculamos a densidade de corrente em módulo como:
Passo 3
Tudo certo até aqui? Agora só falta um detalhe: reparem que o enunciado pede o vetor . Seu sentido é aquele para onde a corrente flui (lembrando que corrente não é vetor!).
Assim sendo, chegamos em:
Resposta
O vetor densidade de corrente na região é dado por: