Dado um conjunto de funções , chamamos de Wronskiano o determinante de ordem , formado pelas funções na primeira linha, pelas primeiras derivadas dessas funções na segunda linha, e assim por diante, até a derivadas das funções na n-ésima linha.
Sejam as funções: ; e
Determine o Wronskiano em.
( )
( )
( )
( )
( )
Passo 1
Eita enunciado complicado hein?! Mas calma que só parece...
Vamos lá. A questão quer a gente calcule esse determinante chamado Wronskiano.
Bom, primeiro, como temos três funções, que são:
Precisaremos ver como as funções ficarão ao serem derivadas até a segunda derivada.
Passo 2
Agora a gente vai jogar isso tudo na matriz, de acordo com a do enunciado:
Como a questão pediu no ponto em que , vamos substituir e ficar com:
(Obs:
Bom, calculando esse determinante teremos:
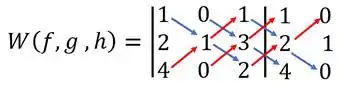
Prontinho! 😊