Determine se as funções dadas são linearmente dependentes ou linearmente independentes no intervalo
Passo 1
Fala aí, tudo beleza?
Observando as funções dadas no problema, não tem nenhuma que podemos desconfiar que seja combinação linear das outras. Logo, para verificar a independência linear, vamos ter de calcular o Wronskiano das funções.
Passo 2
Para calcular o Wronskiano de 3 funções precisaremos fazer o determinante dessa matriz aqui:
Portanto vamos começar calculando as derivadas de primeira e segunda ordem das funções dadas. Em todas elas vamos usar a regra do Tombo, assim: .
Para :
Derivando de novo...
Passo 3
Para :
Derivando de novo...
Passo 4
Para :
Derivando de novo:
Passo 5
Vamos calcular o Wronskiano agora:
Para o cálculo do determinante de uma matriz , nós copiamos as duas primeiras colunas do lado direito da matriz e fazemos as multiplicações das diagonais descendo e subtraímos das multiplicações das diagonais subindo. Assim:
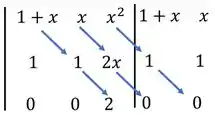
Entãoooo... como o cálculo do Wronskiano é diferente de zero no intervalo , podemos afirmar que e são Linearmente Independentes. 😊
Resposta
e são Linearmente Independentes.