Os dados do último exercício foram tirados das funções abaixo. Calcule o erro absoluto das suas aproximações do exercício e encontre limitantes para o erro.
Passo 1
Relembrando as aproximações que encontramos no último exercício:
O valor exato vai ser:
Passo 2
Agora temos que encontrar o limitante para o erro usando a fórmula
Onde e tem seu módulo máximo no intervalo em e seu módulo máximo no intervalo em :
Substituindo nas fórmulas:
Passo 3
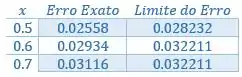
Organizando numa tabelinha:
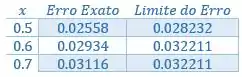
Passo 4
As aproximações que encontramos no último exercício foram:
O valor exato vai ser:
Passo 5
Agora vamos encontrar o limitante para o erro usando a fórmula
Onde e tem seu módulo máximo no intervalo em e seu módulo máximo no intervalo em :
Substituindo nas fórmulas:
Passo 6
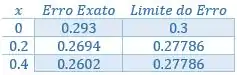
Organizando numa tabelinha:
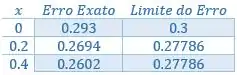
Resposta
Exercícios de Livros Relacionados
27. Deduza a aproximação (2) para y ' ' ( x i ) usando a aproximação de y ( x ) por p 2 ( x ) conforme sugerido no texto.