Uma das aplicações que envolvem o cálculo de determinantes de uma matriz de ordem 3 é o cálculo de volume dos vetores escritos na forma matricial. A partir deste cálculo, principalmente na engenharia, podemos projetar a quantidade de material necessário na confecção de peças em geral. Na perspectiva, retomando o processo de cálculo, leia a questão a seguir e assinale a alternativa CORRETA, sendo
Passo 1
Opaaa! Tudo certinho? Vamos pra mais uma questão de determinantes!
Temos que a nossa matriz é essa daqui!
Para acharmos o determinante de uma matriz, 3x3 existem vários métodos. O que vamos usar aqui é o mais famoso, o método de Sarrus!
Passo 2
Primeiro, vamos repetir as primeiras duas colunas da esquerda
Passo 3
Segundo, vamos traçar linhas na diagonal principal e nas duas diagonais seguintes
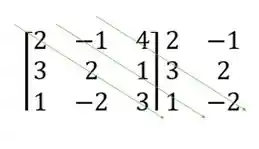
Multiplicar os números que estão na mesma seta e atribuir a eles o sinal de mais
Ajeitando isso, temos que
Passo 4
Depos vamos fazer a mesma coisa com a diagonal secundária e as duas seguintes
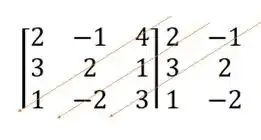
Multiplicando os números que estão na mesma seta e atribuindo a eles o sinal de
Passo 5
Por ultimo é só somar e achar o determinante!
Bora continuar praticando!