Calcule o determinante da matriz
Passo 1
Faaala aí!! Vamos seguir com nossos exercícios de determinantes! Essa matéria é muita prática para ficar fera!
Temos que a nossa matriz é essa daqui!
Vamos usar o método de Sarrus!
Passo 2
Primeiro, vamos repetir as primeiras duas colunas da esquerda
Passo 3
Segundo, vamos traçar linhas na diagonal principal e nas duas diagonais seguintes
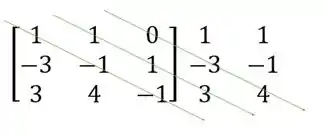
Multiplicar os números que estão na mesma seta e atribuir a eles o sinal de mais
Ajeitando isso, temos que
Passo 4
Depos vamos fazer a mesma coisa com a diagonal secundária e as duas seguintes
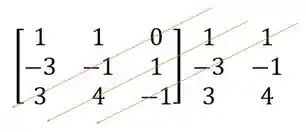
Multiplicando os números que estão na mesma seta e atribuindo a eles o sinal de
Passo 5
Por ultimo é só somar e achar o determinante!
Bora continuar praticando!