Encontre o valor de na matriz abaixo, sabendo que o determinante
Passo 1
Faala ai galerinha, vamos partir pra cima de mais uma questão de determinantes!
Bom, o enunciado diz pra gente que o determinante vale , ou seja
E ele quer descobrir o valor de
Vamos usar o método de Sarrus! Se liga aqui como a gente vai resolver isso!
Passo 2
Primeiro, vamos repetir as primeiras duas colunas da esquerda
Passo 3
Segundo, vamos traçar linhas na diagonal principal e nas duas diagonais seguintes
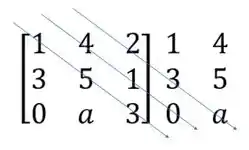
Multiplicar os números que estão na mesma seta e atribuir a eles o sinal de mais
Realizando esses produtos, temos
Passo 4
Depos vamos fazer a mesma coisa com a diagonal secundária e as duas seguintes
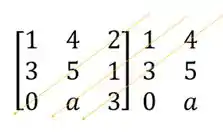
Multiplicando os números que estão na mesma seta e atribuindo a eles o sinal de
Passo 5
Por ultimo é só somar tudo e achar o determinante!
Passo 6
Mas o enunciado diz que
Então, temos que