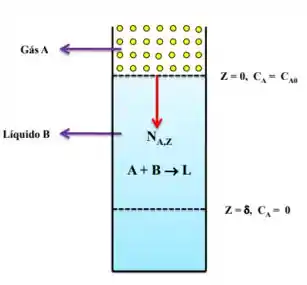
Um certo gás é dissolvido em um líquido B contido em uma proveta. Na medida em que A difunde ele sofre reação química na forma , até desaparecer completamente depois de penetrar a uma distância desde a interface gás/líquido. Considerando:

1. a cinética de reação é de ordem zero com respeito a A;
2. reação química lenta ;
3. a concentração do gás A dissolvido é pequena se comparada ao do líquido B;
4. o produto da reação L é altamente solúvel no líquido, o que leva a não influenciar na difusão do soluto A; obtenha expressões para:

• A distribuição da concentração molar de A;
• O fluxo global molar de A na interface gás/líquido;
• A concentração média molar de A.

Agora é a hora de estabelecer nossas condições de contorno, pra que a gente descubra quem são e …

A nossa primeira condição de contorno, será na interface gás/líquido, onde:

Temos então:

Isso nos diz que:

E usando a segunda condição de contorno, que é quando o soluto é totalmente consumido, temos:

Isso quer dizer que temos:

Substituindo o , vamos ter:

O será então:

Agora substituindo e na equação que a gente tinha antes, ficaremos com:

Por fim, como estamos trabalhando com uma reação química lenta, então , e rearranjando essa galera, a distribuição da concentração molar do reagente “A” será:

Partiu encontrar o fluxo molar! Ele vai ser dado pela equação:

E se a gente voltar lá na equação:

E derivar ela em função de , vamos ter:

E como estamos buscando o fluxo na interface gás/líquido, , temos:

E substituindo isso na equação do fluxo, vamos ficar com:

E como , por ser uma reação lenta, temos que o fluxo molar será:

Só falta a gente encontrar a concentração média molar… Temos que:

Substituindo a nossa equação , vamos ter:

Isso nos dá:

E como a gente já falou antes, , logo a concentração média molar é:

Arrasamos! Foi grande, mas conseguimos!