Considere um reator catalítico onde se realiza uma reação irreversível do tipo:
Imagine que a partícula catalítica esteja rodeada por uma película gasosa através do qual difunde o reagente A até alcançar a superfície não-porosa do catalisador. Suponhamos que a reação ocorra instantaneamente sobre a superfície do catalisador e que o produto “B” difunda no sentido contrário do reagente “A”. Considerando o processo de transferência de massa em regime permanente e a T e P constantes e que a reação ocorra sobre uma superfície plana do catalisador, determine o perfil da fração molar e o fluxo molar do soluto “A” em função da espessura da película gasosa “”.
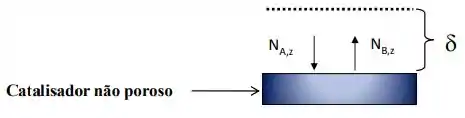
Passo 1
Show de bolinhas! Então nós temos uma superfície catalítica, estilo plana plana, onde ocorre a reação:
Certo? E nosso enunciado pede pra gente o perfil da fração molar e o fluxo molar, sendo a pressão e a temperatura constantes… Humm… Nossa solução então deve obedecer a seguinte equação:
Mas tá enorme isso aí, né? Vamos fazer algumas considerações, beleza?
A primeira é que estamos trabalhando em regime permanente, então: ;
A segunda é que o fluxo de , vai ser apenas na direção , então: ∇;
E a terceira é que não temos reação química homogênea, logo:
Com essas considerações nossa equação, vai ficar com essa cara aqui:
Teremos assim, um fluxo total até a superfície do catalisador, igual a:
E pela estequiometria da nossa reação, temos:
E substituindo isso ali em cima, vamos ter:
Arrumando essa equação, teremos:
Ficamos então com:
E como vimos que , ficamos com:
E como nosso enunciado disse que temos pressão e temperatura constantes, nosso e , também vão ser constantes, logo:
Integrando isso aí, vamos ficar com:
E integrando novamente:
Ficaremos então, com:
Passo 2
Agora vamos aplicar algumas condições de contorno! A primeira é que:
Em:
Opa! Então vamos ter que:
Vamos ter então:
E usando a segunda condição de contorno, devido a reação ser instantânea, temos que:
Em:
Isso quer dizer que:
Substituindo o que já encontramos, ficaremos com:
Agora vamos substituir e na equação que a gente tinha antes, teremos então:
Vamos dividir todos os termos por 2 para simplificar, ok?
E pela “regra do peteleco”:
Show! Vamos ficar então:
Opa! Já encontramos a expressão para o perfil da fração molar! Agora falta o fluxo … Vamos nessa!
Passo 3
Se a gente considerar um fluxo constante sobre a superfície do catalisador, vamos ter:
contante
Integrando a gente vai ficar com:
Nosso fluxo, será então:
Conseguimos!!
Resposta
Perfil da fração molar:
Fluxo de :