Uma partícula de carbono em forma de esfera queima no ar através da seguinte reação química:
A reação na superfície do carbono é descrita como sendo irreversível e de primeira ordem:
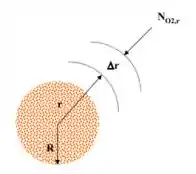
Considerando que o processo de transferência de massa ocorra em regime permanente e a e constante, determine o perfil de fração molar do oxigênio em função do raio da partícula esférica e o fluxo molar do oxigênio na superfície da partícula de carbono.
Passo 1
Bom, como a nós temos uma partícula que é esférica vamos usar a equação em coordenadas esféricas, ok? Olha ela aqui:
Fazendo algumas considerações…
Como estamos trabalhando em regime permanente, então: ;
O fluxo é radial e unidirecional, então: ∇;
E como temos um meio difusivo e não reacional:
Com essas considerações nossa equação, vai ficar com essa cara aqui:
A equação reacional é:
![]()
Temos então:
Como C é sólido, então:
E tendo a partícula estagnada, então:
Sendo assim, ficamos com:
Logo, o fluxo total de , em meio gasoso, fica:
E se , então ficamos com:
E substituindo isso ali em cima, vamos ter:
Como o enunciado disse pra gente que estamos trabalhando com pressão e temperatura constantes, então sabemos que e também são constantes, a equação vai fica então:
Integrando isso aí, vamos ficar com:
E integrando novamente:
Ficaremos então, com:
Passo 2
Agora é a hora de estabelecer nossas condições de contorno, pra que a gente descubra quem são e …
A nossa primeira condição de contorno é que:
Em:
Temos então:
Sendo assim:
E usando a segunda condição de contorno:
Em:
Isso quer dizer que:
Substituindo o que já encontramos, ficaremos com:
O será então:
Agora vamos substituir e na equação que a gente tinha antes, ficaremos com:
Rearranjando, temos:
O perfil da fração molar, será então:
Agora partiu achar o fluxo !
Passo 3
Se a gente considerar um fluxo total constante em , vamos ter:
constante
Sendo a área da esfera, ficaremos com:
constante
Agora vamos multiplicar a equação que a gente tinha antes pela área da esfera:
Ficaremos com:
Integrando a gente vai ficar com:
Nosso fluxo, será então:
Show de bola! E a gente ainda pode substituir o fluxo no perfil de fração molar e ficar com:
Reorganizando e fazendo as simplificações necessárias, ficamos com:
Logo, nosso perfil de fração molar ficará:
Prontinhos! Terminamos!
Resposta
Perfil da fração molar:
Fluxo: