Uma corrente gasosa contendo um reagente “A” entra em contato com um catalisador de geometria esférica de raio R. Esta partícula está dentro de um reator catalítico. Nas imediações da partícula catalítica, a concentração do reagente “A” é (moles/cm3 ). A espécie “A” difunde através dos poros existentes no catalisador e converte no produto “B” através de uma reação irreversível e de primeira ordem no sítio ativo do mesmo. O produto “B” difunde no sentido contrário do reagente “A”. Determine o perfil de concentração do reagente “A” em função do raio da partícula considerando que o processo de transferência de massa ocorra em regime permanente e a temperatura e pressão constante.
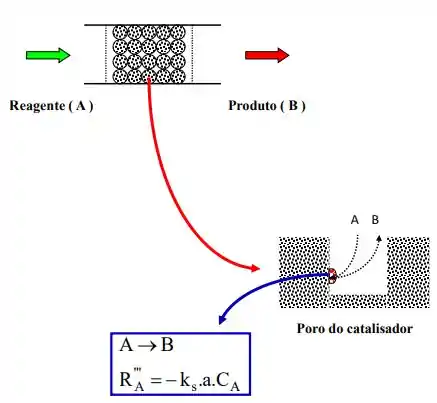
Sendo:
área da superfície catalítica por unidade de volume do catalisador
constante de velocidade
concentração do reagente
Passo 1
Mais uma vez vamos trabalhar com a equação em coordenadas esféricas:
Fazendo nossas considerações…
Como estamos trabalhando em regime permanente, então: ;
O fluxo é radial e unidirecional, então: ∇;
E considerando que a reação acontece dentro do poro do catalisador, temos que:
Sendo assim nossa equação, fica:
O fluxo molar no interior da parte porosa, levando em conta o coeficiente de difusão efetiva, , será:
Sendo:
Onde porosidade do catalisador e tortuosidade do catalisador.
E sendo , nossa equação será:
Agora substituindo isso na equação ali de cima, vamos ter:
Como o enunciado disse pra gente que estamos trabalhando com pressão e temperatura constantes, então sabemos que também é constante, ficamos então com:
Chamando , teremos:
Precisamos encontrar um jeito de melhor essa equação, porque esse vai nos atrapalhar nas integrações, ok? Vamos fazer o seguinte então:
Teremos então que:
Substituindo isso na nossa equação, ficaremos com:
Integrando isso aí, duas vezes, vamos ficar com:
Agora voltando com o , vamos ter:
Passo 2
Agora é a hora de estabelecer nossas condições de contorno, pra que a gente descubra quem são e …
A nossa primeira condição de contorno, se refere a entrada do poro, onde:
Temos então:
E usando a segunda condição de contorno, que se refere ao centro da partícula catalítica, temos:
Isso quer dizer que temos:
O será então:
Agora vamos substituir lá na primeira condição de contorno, beleza?
Logo, o vai ser:
Agora substituindo e na equação que a gente tinha antes, ficaremos com:
Por fim, rearranjando essa galera, o perfil de concentração do reagente “A” em função do raio da partícula será:
Uhull! Conseguimos!
Resposta
O perfil de concentração do reagente “A” em função do raio da partícula: