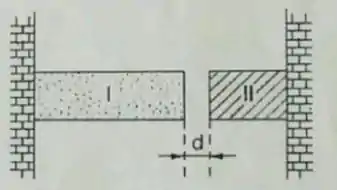
Considere um microssistema abaixo formado por duas pequenas peças metálicas, e , presas em duas paredes laterais. Observamos que, na temperatura de , a peça tem tamanho igual a , quanto a peça tem apenas de comprimento. Ainda nesta temperatura as peças estavam afastadas apenas por uma pequena distancia igual a . Sabendo-se que o coeficiente de dilatação da pela é igual a e que o da peça é igual a . Qual deve ser a temperatura do sistema, em , para que as duas peças entrem em contato sem empenar?
Passo 1
Faaala galerinha, temos ai mais uma questão de dilatação térmica!
Vamos começar fazendo o que? Se você disse separando as informações do enunciado, acertou!! Vambora então! A gente tem que
Para peça
Para peça
Para as duas peças:
Vamos ter então que
Passo 2
Show galerinha, vamos analisar mais um pouco esse enunciado, ele quer a temperatura pras placas se encontrarem, ou seja, ele quer que a dilatação seja igual a !Para isso acontecer a gente precisa que
E quem é esse
Vai ser a soma das dilatações, então temos
Passo 3
Show, vamos calcular então esses nossos ’s
Comecando pelo
Fazendo a distributiva, temos que
Show, vamos guardar esse resultado e partir agora para
Fazendo a distributiva, temos que
Passo 4
Show, achamos os dois , vamos lembrar que
Substituindo isso daí, ficamos com
Vamos ajeitar o lado esquerdo, juntando o que tem e o que não tem
Vamos passar tudo pra mesma potência de , ajeitando o lado direito, temos
Ufa, podemos sumir com essas potências feias, pra ficar mais bonitinho de visualizar
Passando o pro outro lado, temos
Passando esse dividindo, temos:
Isso nos dá: