A figura a seguir ilustra três barras de seção quadrada com lado igual a 10 cm posicionadas entre os cabeçotes de uma prensa hidráulica. Duas barras são constituídas por um material B e a outra por um material A.
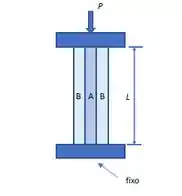
Sabe-se que o material A possui módulo de elasticidade igual a 200 GPa, enquanto o material B possui módulo de elasticidade igual a 100 GPa. Além disso, a distância entre os cabeçotes, L, é igual a 1,0 m.Ao se impor uma carga P igual a 2000 kN, calcule a deformação específica provocada por essa força em % apenas em A.
Passo 1
Então, como a gente já sabe:
A questão quer a deformação... Então ela quer esse termo aqui ó:
Então pra descobrir esse termo, precisamos do módulo de elasticidade (que a questão já nos deu) e da tensão, que não temos, mas temos a força e podemos calcular a área tramsversal, sacou? Como a áre transversal é quadrada e de lado 0,1m, temos que a área é 0,01. Show! Então nossa tensão é:
Show, né? Agora como queremos a deformação em A, é só usarmos o módulo de elasticidade do material A:
Então a deformação foi de . Pequenininha, né não? :p