Um pedaço de arame recozido de aço baixo carbono tem 2 mm de diâmetro, limite de escoamento (elásticidade) 210MPa e módulo de elasticidade 207GPa. Pergunta-se:
a) Se uma garota de 54 kg se dependura neste arame, ocorrerá deformação plástica (defor no arame?
b) Se for possível com os dados disponíveis no problema, calcule o alongamento porcentual do arame com a garota dependurada.
Passo 1
Como a gente viu lá no graficozinho, a deformação plástica (ou faixa permanente) é logo após o limite de elasticidade, né? Então como a gente tem a massa da garota, é so analisarmos a tensão que a força Peso dela vai exercer no arame de aço e vermos se essa tensão é superior ao limite, show? Vamo lá:
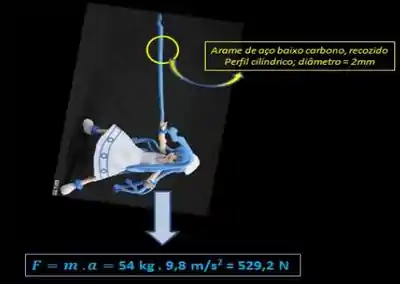
Agora é só calcular a tensão!
Como o módulo da nossa tensão é menor que o limite elástico (210MPa) não ocorre deformação plástica, apenas elástica! Simboraaaa!
Passo 2
Agora calcular a porcentagem da deformação ficou fácil, né? Bora lá:
Chamando o alongamento de , temos:
Como queremos em pocentagem, é só multiplicarmos por 100, então temos: