Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Potencial

Ver Teoria
Exercício 31245678

Enunciado

A barra uniforme de massa m e comprimento l é articulada em relação a um eixo horizontal que passa pela sua extremidade O e está presa a uma mola de torção, que exerce um torque M = K θ sobre ela, onde K é a rigidez da mola, expressa em unidades de torque por radianos, e θ é a deflexão angular em relação à vertical, medida em radianos. Determine o valor máximo de l , para o qual o equilíbrio na posição θ = 0 é estável.

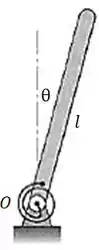
Passo 1

A energia potencial associada à mola é dada por:

V e l = K θ 2 2

Repare que trocamos o x por θ , pois neste caso temos rotação θ da mola!

E a energia potencial gravitacional da barra?

Bom, vai ser dada pelo produto da massa, da gravidade e da altura do centro de gravidade:

V g = m g h

Para achar a altura do centro de gravidade vamos usar trigonometria:

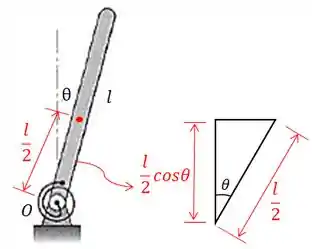
Então:

h = l c o s θ 2

Substituindo na nossa fórmula, vamos ter que:

V g = m g h       →         V g = m g l 2 c o s θ

Passo 2

A energia total V será a soma das energias que achamos:

V = V e l + V g

∴

V = K θ 2 2 + m g l 2 c o s θ

Passo 3

Agora temos que derivar com relação a θ a expressão da energia total que achamos:

d V d θ = K θ - m g l 2 s e n θ

∴

d 2 V d θ 2 = K - m g l 2 c o s θ

Passo 4

Para que em θ = 0 exista uma equilíbrio devemos ter que:

d V 0 d θ = 0

Vamos ver se esta condição já foi satisfeita:

d V 0 d θ       →         K 0 - m g l 2 s e n 0 = 0

Então, a condição para ter equilíbrio foi satisfeita!

Passo 5

E para que este equilíbrio seja estável precisamos atender a esta condição aqui:

d 2 V 0 d θ 2 > 0

Então, vamos ter que derivar novamente a nossa expressão da energia total:

d 2 V d θ 2 = K - m g l 2 c o s θ

Agora vamos ver qual a condição para termos o equilíbrio estável:

d 2 V ( 0 ) d θ 2 > 0

∴

K - m g l 2 c o s ⁡ ( 0 ) > 0

∴

K - m g l 2 > 0       →             l < 2 K m g

Resposta

l < 2 K m g

Exercícios de Livros Relacionados

49- U m pequeno elevador industrial, acionado a pedal, está mostrado na figura. Existem quatro molas idênticas, duas de cada lado do eixo central. A rigidez de cada par de molas vale 2 k . Ao projetar
A barra uniforme A B pesa 500 N . Se as duas molas D EeB C estão livres quando θ = 90 ° , determine o ângulo θ para equilíbrio usando o princípio da energia potencial. Investigue a estabilidade na pos
Determine a altura h do bloco B de modo que a barra esteja sempre em equilíbrio. As molas estão livres quando a barra está na posição vertical. O bloco tem um peso W .
A mola conectada ao mecanismo tem um comprimento livre quando θ = 90 ° . Determine a posição θ para o equilíbrio e investigue a estabilidade do mecanismo nessa situação. O disco A é conectado por pino
47- A seção transversal de um basculante articulado em relação ao eixo horizontal O , de massa m e com centro de massa em G , está mostrada na figura. A medida que o basculante abre, a mola é comprimi