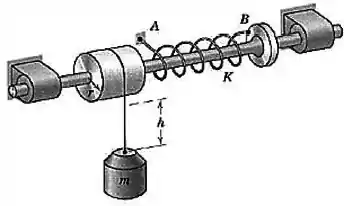
Uma extremidade da mola de torção está presa ao chão em e a outra extremidade está presa ao eixo em . A rigidez à torção da mola elástica é o torque necessário para torcer a mola de um ângulo de um radiano. A mola resiste ao momento em torno do eixo, causado pela força de tração no cabo enrolado ao redor do tambor de raio . Determine o valor de equilíbrio de medido a partir da posição tracejada, na qual a mola não está torcida.
Passo 1
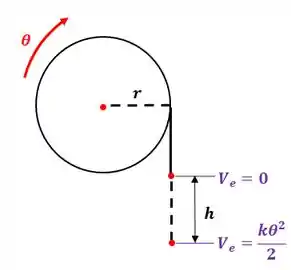
O sistema pode ser representado pelo desenho abaixo:
Passo 2
Temos duas energias potenciais...
A primeira é a energia potencial gravitacional:
E a segunda é a energia potencial elástica:
Então, para acharmos a expressão da energia total é só somarmos cada uma das energias:
Passo 3
Agora precisamos derivar esta equação com relação ao ângulo :
Como o sistema está em equilíbrio precisamos igualar a zero a equação que acabamos de achar:
A distância que a corda andou corresponde ao comprimento :
Substituindo isso na expressão que achamos, vamos ter que: