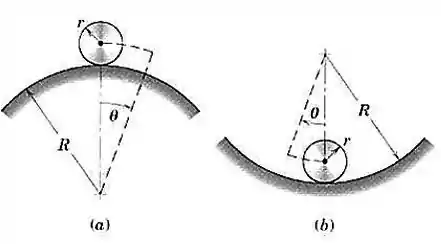
O pequeno cilindro de massa e raio está confinado a rolar sobre a superfície circular de raio . Usando os métodos desta seção, prove que o cilindro é instável no caso e estável no caso
Passo 1
Vamos considerar que é o nível de energia potencial nula no nosso sistema. Então, podemos desenhar o caso assim:
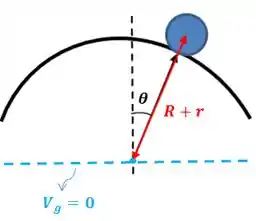
A energia potencial gravitacional do cilindro é calculada pela seguinte fórmula:
Onde é a distância vertical do centro de massa do cilindro até o nosso ponto onde a energia potencial é nula:
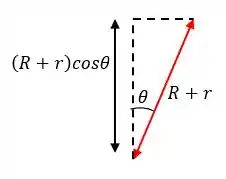
Então:
Com isso conseguimos calcular a energia potencial gravitacional do cilindro:
Passo 2
No outro caso temos o seguinte:
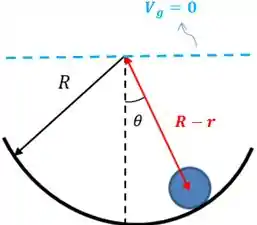
E a altura do centro de gravidade do cilindro?
Por que está negativo? Porque a altura está abaixo da nossa referência que é quando .
Dessa forma, a energia potencial gravitacional será:
Passo 3
Vamos testar os dois casos. Para isso temos que derivar a equação da energia potencial.
Vamos começar com o caso . Sabemos que a energia potencial gravitacional neste caso é:
Então, a derivando isso com relação a vamos ter que:
Para termos equilíbrio precisamos igualar esta equação a zero, então:
O é zero em duas situações, quando:
Neste caso, tem que ser rejeitado porque não faz muito sentido. É como se a massa estivesse dentro da curva onde o cilindro se encontra.
Agora temos que derivar de novo para analisar a estabilidade:
Agora vamos substituir nesta expressão que acabamos de achar:
Repare que o resultado será negativo, então ele será sempre menor que zero e isso caracteriza a situação do equilíbrio instável!
Passo 4
Vamos fazer o mesmo processo para o segundo caso. A equação da energia potencial que achamos foi:
Agora vamos derivar ela com relação à :
Para termos equilíbrio precisamos igualar esta equação a zero, então:
O é zero em duas situações, quando:
Novamente vamos descartar a solução !
Agora temos que derivar de novo para analisar a estabilidade:
Agora vamos substituir nesta expressão que acabamos de achar:
Repare que o resultado será positivo, então ele será sempre maior que zero e isso caracteriza a situação do equilíbrio estável!