O sistema formado por uma barra leve articulada, a massa da extremidade e a mola, de rigidez são mostradas em sua posição de equilíbrio. O parâmetro é uma fração situada na faixa . Mostre que o sistema é estável para todos os valores de na faixa permissível.
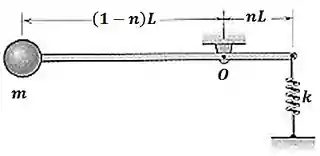
Passo 1
Vamos primeiro usar o equilíbrio de momentos para descobrir o deslocamento da mola, , para a situação em que o ângulo vale
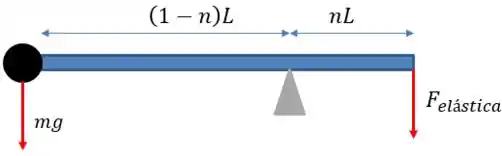
Temos:
Mas sabemos que a força elástica é calculada pela seguinte equação:
Assim:
Onde é a distensão da mola quando a barra está na horizontal
Passo 2
Agora vamos analisar o problema para um caso em que
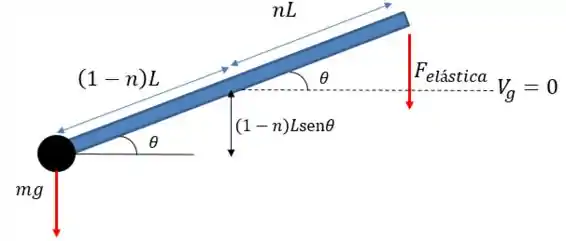
Veja que o nível zero da energia potencial está no centro de giro da barra, ou seja, no ponto . Assim, a energia potencial da massa será:
Onde é a distância do centro de gravidade da massa até o nosso ponto de referência que é onde , então:
Repare que o sinal é negativo, pois o centro de gravidade está abaixo do nosso referencial!
Então, a energia potencial gravitacional será:
Já a energia potencial da mola, será:
Onde é o comprimento da mola quando a barra está na horizontal mais o quanto ela esticou que é :
Então, a energia potencial elástica é:
Agora somamos a energia potencial gravitacional e a elástica para acharmos a energia potencial total ():
Arrumando isso melhor, vamos ter que:
Passo 3
Agora temos que derivar esta equação que achamos:
Para que haja equilíbrio, devemos igualar o que achamos a zero:
Para que nossa expressão seja zero, devemos ter que:
Ou seja, em há equilíbrio. Partimos do caso geral e descobrimos que é a posição de equilíbrio.
Passo 4
Vamos derivar duas vezes a expressão da energia total:
E precisamos substituir para vermos o que acontece:
Como é sempre maior que zero da mesma forma que e também serão, então podemos dizer que:
para