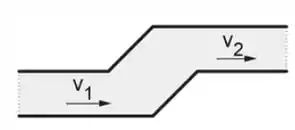
Um engenheiro trabalha em uma indústria que contém grandes tubulações de água, usada para resfriar um tanque no qual ocorrem reações exotérmicas. Em determinado ponto, a tubulação eleva-se em , como ilustra a figura. Existem sensores de pressão na tubulação em ambas as alturas, que indicam um mesmo valor na leitura. Ele precisa conhecer a velocidade da água no nível mais alto, sabendo que ela entra no nível mais baixo com velocidade . Ele sabe que a água pode ser considerada um fluido aproximadamente incompressível e com baixa viscosidade.

Animados para mais umaa?!

Bom galerinha, problemas com esta carinha aí vocês já sabem que podemos usar a famosa Equação de Bernoulli:

O problema nos contou que em ambos os pontos a pressão é a mesma:

Na equação:

Se o termo está presente dos dois lados da igualdade, com o mesmo sinal () eles vão se cancelar:

Agora podemos assumir que o ponto mais baixo terá altura igual a zero, só para facilitar nossas contas:

Substituindo:

Se a densidade está presente em todos os termos, podemos cortar:

Aos pouquinhos nossa equação gigantesca vai diminuindo. Precisamos achar o que mesmo?

A velocidade no ponto mais alto, ou seja, !! Vamos isolá-la passando o termo para o outro lado com sinal oposto:

O que está dividindo, faz o que? Passa para o outro lado multiplicando:

Agora o multiplica cada termo dentro do parênteses:

Aplicamos a raiz dos dois lados:

Shooow!! Encontramos uma fórmula para calcular a velocidade!