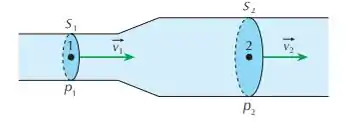
Um líquido de densidade flui pelo tubo indicado na figura, passando pelo ponto com velocidade e pelo ponto com velocidade . A pressão no ponto é . Determine:
- a razão entre as áreas das seções transversais e ;
- a pressão no ponto .
Passo 1
Vamos continuando?
A primeira coisa que o problema nos pediu foi a razão entre as áreas das seções transversais e , certo? Mas o que seria essa razão? A razão é nada mais, nada menos, que a divisão entre as áreas e . Ou seja, estamos interessados em calcular
De cara a Equação de Bernoulli não nos ajuda porque não tem as áreas na equação
Mas temos a Equação da Continuidade, não é? E acabamos de ver que ela é dada por:
Como o que queremos é , vamos passar a área da seção transversal dividindo para o outro lado:
E essa velocidade aí também passa para o outro lado dividindo, certo?
O problema nos disse que:
Substituindo:
Show! A letra (a) já foi para o saco.
Passo 2
Para calcular a letra (b) precisamos achar a pressão no ponto , certo?
E agora sim é a vez dela, a Equação de Bernoulli!!
Pelo desenho vemos que a altura do ponto central de cada seção é igual:
Substituindo:
Como o termo está presente nos dois lados com o mesmo sinal (), eles se cancelam:
Sabendo que:
Só nos resta substituir, não é?
O termo passa para o outro lado da igualdade com sinal contrário:
Chegamos ao final de mais umaa!!