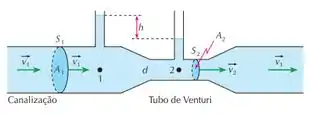
Pretende-se medir a vazão de um líquido que escoa por uma canalização. Para isso, utiliza-se um aparelho chamado tubo de Venturi, que consiste essencialmente de um tubo cujas seções e têm áreas e conhecidas. A diferença de pressão entre os pontos e é medida por meio do desnível do líquido existente nos tubos verticais. O tubo de Venturi é inserido na canalização, conforme mostra a figura. Sendo , , , e a densidade do líquido, determine a vazão do líquido através da canalização.
Passo 1
Galerinhaa do meu coração, essa aqui é um pouco diferente das demais, não é?
Mas não vamos nos assustar!!
O problema nos pediua a vazão, e como vimos na Equação da Continuidade que pode ser calculada como:
Também podemos usar o ponto , porque a vazão que entra em tem que sair em , não é?!
Beleza! A área nós temos, mas nada de velocidade ainda
Que tal usarmos aqui a Equação de Bernoulli?
A altura do ponto central das duas seções é a mesma, então:
Na fórmula:
Como o termo está nos dois lados da igualdade com o mesmo sinal podemos cancelar:
Temos quase nada! Eita lasqueira!!
Mas vamos fazer uma manipulação matemática e mandar a pressão de para o outro lado da igualdade com sinal contrário, assim como o termo
Essa variação de pressão nós temos uma fórmula para ela, não é?
Se não se lembram, eu mostro pra vocês:
Então:
Como a densidade está presente em todos os termos, vamos cortar:
Multiplicando todos os termos por para facilitar a nossa vida lá na frente:
Passo 2
Ainda não dá para calcular a velocidade com o que temos até agora ☹
Camos recorrer a equação da continuidade!
Isolando a velocidade no ponto , vamos passar a área para o outro lado dividindo:
As áreas nós temos, não é?
Então:
E substituindo isso na equação do Passo :
Passamos o para o outro lado dividindo:
Tiramos a raiz dos dois lados:
Sabendo que:
Substituindo:
Passo 3
Achamos o que queríamos?
Que nada!! Queremos a vazão
Sabemos que:
Vamos precisar transformar esse aí em , ok? Se lembram da transformação?
Então:
Agora que temos tudo, basta substituir:
Podemos deixar assim, ou transformar em , lembrando que:
Então:
Gostaram dessa ?!